
【题目】如图,在直二面角D﹣AB﹣E中,四边形ABCD是边长为2的正方形,AE=EB,点F在CE上,且BF⊥平面ACE; 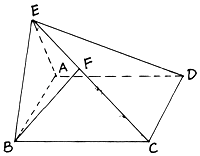
(1)求证:AE⊥平面BCE;
(2)求二面角B﹣AC﹣E的正弦值;
(3)求点D到平面ACE的距离.
【答案】
(1)证明:∵BF⊥平面ACE,∴BF⊥AE,
∵二面角D﹣AB﹣E为直二面角,
∴平面ABCD⊥平面ABE,
又BC⊥AB,∴BC⊥平面ABE,则BC⊥AE,
又BF平面BCE,BF∩BC=B,
∴AE⊥平面BCE
(2)法一、解:连接AC、BD交于G,连接FG,
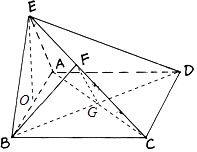
∵ABCD为正方形,∴BD⊥AC,
∵BF⊥平面ACE,BG⊥AC,∴AC⊥平面BFG,
∴FG⊥AC,即∠FGB为二面角B﹣AC﹣E的平面角,
由(1)可知,AE⊥平面BCE,∴AE⊥EB,
又AE=EB,AB=2,AE=BE= ![]() ,
,
在直角三角形BCE中,CE= ![]() =
= ![]() ,BF=
,BF= ![]() =
= ![]() ,
,
在正方形中,BG= ![]() ,在直角三角形BFG中,sin∠FGB=
,在直角三角形BFG中,sin∠FGB= ![]() ;
;
法二、以线段AB的中点为原点O,OE所在直线为x轴,AB所在直线为y轴,
过O点平行于AD的直线为z轴,建立空间直角坐标系O﹣xyz,如图.
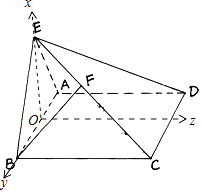
∵AE⊥面BCE,BE面BCE,∴AE⊥BE,
在Rt△AEB中,AB=2,O为AB的中点,
∴OE=1.∴A(0,﹣1,0),E(1,0,0),C(0,1,2),
![]() =(1,1,0),
=(1,1,0), ![]() =(0,2,2).
=(0,2,2).
设平面AEC的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
则 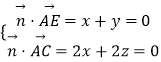 ,令x=1,得
,令x=1,得 ![]() =(1,﹣1,1)是平面AEC的一个法向量.
=(1,﹣1,1)是平面AEC的一个法向量.
又平面BAC的一个法向量为 ![]() =(1,0,0),
=(1,0,0),
∴cos< ![]() >=
>= ![]() =
= ![]() .
.
∴二面角B﹣AC﹣E的正弦值为 ![]()
(3)法一、由(2)可知,在正方形ABCD中,BG=DG,D到平面ACE的距离等于B到平面ACE的距离,
BF⊥平面ACE,线段BF的长度就是点B到平面ACE的距离,即为D到平面ACE的距离所以D到平面的距离为 ![]() .
.
法二、
解:∵AD∥z轴,AD=2,∴ ![]() =(0,0,2),
=(0,0,2),
∴点D到平面ACE的距离d=| ![]() ||cos<
||cos< ![]() >=
>= ![]() =
= ![]() .
.
【解析】(1)要证AE⊥平面BCE,只需证明AE垂直平面BCE内的两条相交直线BF、BC即可;(2)连接AC、BD交于G,连接FG,说明∠FGB为二面角B﹣AC﹣E的平面角,然后求二面角B﹣AC﹣E的大小;(3)利用VD﹣ACE=VE﹣ACD , 求点D到平面ACE的距离,也可以利用空间直角坐标系,向量的数量积,证明垂直,求出向量的模.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣3x.
(1)求曲线y=f(x)在点x=2处的切线方程;
(2)若过点A(1,m)(m≠﹣2)可作曲线y=f(x)的三条切线,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(ax2+4x+5).
(1)若f(1)<3,求a的取值范围;
(2)若a=1,求函数f(x)的值域.
(3)若f(x)的值域为R,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+φ),其中φ为实数,若f(x)≤|f( ![]() )|对x∈R恒成立,且f(
)|对x∈R恒成立,且f( ![]() )>f(π),则f(x)的单调递增区间是( )
)>f(π),则f(x)的单调递增区间是( )
A.[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
B.[kπ,kπ+ ![]() ](k∈Z)
](k∈Z)
C.[kπ+ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
D.[kπ﹣ ![]() ,kπ](k∈Z)
,kπ](k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)的导函数y=f′(x)的图象如图所示,则关于函数y=f(x),下列说法正确的是( ) 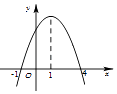
A.在x=﹣1处取得极大值
B.在区间[﹣1,4]上是增函数
C.在x=1处取得极大值
D.在区间[1,+∞)上是减函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+c在x=﹣ ![]() 与x=1时都取得极值.
与x=1时都取得极值.
(1)求a、b的值与函数f(x)的单调区间;
(2)若对x∈[﹣1,2],不等式f(x)<c2恒成立,求c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com