
【题目】在空间中,过点A作平面π的垂线,垂足为B,记B=fπ(A).设α,β是两个不同的平面,对空间任意一点P,Q1=fβ[fα(P)],Q2=fα[fβ(P)],恒有PQ1=PQ2 , 则( )
A.平面α与平面β垂直
B.平面α与平面β所成的(锐)二面角为45°
C.平面α与平面β平行
D.平面α与平面β所成的(锐)二面角为60°
【答案】A
【解析】解:设P1=fα(P),则根据题意,得点P1是过点P作平面α垂线的垂足
∵Q1=fβ[fα(P)]=fβ(P1),
∴点Q1是过点P1作平面β垂线的垂足
同理,若P2=fβ(P),得点P2是过点P作平面β垂线的垂足
因此Q2=fα[fβ(P)]表示点Q2是过点P2作平面α垂线的垂足
∵对任意的点P,恒有PQ1=PQ2 ,
∴点Q1与Q2重合于同一点
由此可得,四边形PP1Q1P2为矩形,且∠P1Q1P2是二面角α﹣l﹣β的平面角
∵∠P1Q1P2是直角,∴平面α与平面β垂直
故选:A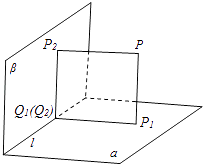
【考点精析】掌握空间中直线与平面之间的位置关系和平面与平面之间的位置关系是解答本题的根本,需要知道直线在平面内—有无数个公共点;直线与平面相交—有且只有一个公共点;直线在平面平行—没有公共点;两个平面平行没有交点;两个平面相交有一条公共直线.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】已知圆C的圆心在x轴正半轴上,半径为5,且与直线![]() 相切.
相切.
(1)求圆C的方程;
(2)设点![]() ,过点
,过点![]() 作直线
作直线![]() 与圆C交于
与圆C交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)设P是直线![]() 上的点,过P点作圆C的切线
上的点,过P点作圆C的切线![]() ,切点为
,切点为![]() 求证:经过
求证:经过![]() 三点的圆必过定点,并求出所有定点的坐标.
三点的圆必过定点,并求出所有定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位招聘员工,有![]() 名应聘者参加笔试,随机抽查了其中
名应聘者参加笔试,随机抽查了其中![]() 名应聘者笔试试卷,统计他们的成绩如下表:
名应聘者笔试试卷,统计他们的成绩如下表:
分数段 |
|
|
|
|
|
|
|
人数 | 1 | 3 | 6 | 6 | 2 | 1 | 1 |
若按笔试成绩择优录取![]() 名参加面试,由此可预测参加面试的分数线为( )
名参加面试,由此可预测参加面试的分数线为( )
A. ![]() 分 B.
分 B. ![]() 分 C.
分 C. ![]() 分 D.
分 D. ![]() 分
分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果某地的财政收入![]() 与支出
与支出![]() 满足线性回归方程
满足线性回归方程![]() (单位:亿元),其中
(单位:亿元),其中![]() ,如果今年该地区财政收入10亿元,则年支出预计不会超过( )
,如果今年该地区财政收入10亿元,则年支出预计不会超过( )
A. 10.5亿 B. 10亿 C. 9.5亿 D. 9亿
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知e为自然对数的底数,设函数f(x)=(ex﹣1)(x﹣1)k(k=1,2),则( )
A.当k=1时,f(x)在x=1处取得极小值
B.当k=1时,f(x)在x=1处取得极大值
C.当k=2时,f(x)在x=1处取得极小值
D.当k=2时,f(x)在x=1处取得极大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查观众对电视剧《风筝》的喜爱程度,某电视台举办了一次现场调查活动.在参加此活动的甲、乙两地大量观众中,各随机抽取了8名观众对该电视剧评分做调查(满分100分),被抽取的观众的评分结果如图所示.

(1)从甲地抽取的8名观众和乙地抽取的8名观众中分别各选取一人,在已知两人中至少一人评分不低于90分的条件下,求乙地被选取的观众评分低于90分的概率。
(2)从甲地抽取出来的8名观众中选取1人,从乙地抽取出来的8名观众中选取2人去参加代表大会,记选取的3人中评分不低于90分的人数为![]() ,求
,求![]() 的分布列与期望。
的分布列与期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=2AA1 , ∠BAC=120°,D,D1分别是线段BC,B1C1的中点,P是线段AD的中点. 
(1)在平面ABC内,试做出过点P与平面A1BC平行的直线l,说明理由,并证明直线l⊥平面ADD1A1;
(2)设(1)中的直线l交AB于点M,交AC于点N,求二面角A﹣A1M﹣N的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com