
【题目】已知:sin230°+sin290°+sin2150°= ![]() ,sin25°+sin265°+sin2125°=
,sin25°+sin265°+sin2125°= ![]() .通过观察上述两等式的规律,请你写出一般性的命题,并给出证明.
.通过观察上述两等式的规律,请你写出一般性的命题,并给出证明.
【答案】解:由已知中sin230°+sin290°+sin2150°= ![]() ,
,
sin25°+sin265°+sin2125°= ![]() .
.
归纳推理的一般性的命题为:
sin2(α﹣60°)+sin2α+sin2(α+60°)= ![]() .
.
证明如下:
左边= ![]() +
+ ![]() +
+ ![]()
= ![]() ﹣
﹣ ![]() [cos(2α﹣120°)+cos2α+cos(2α+120°)]
[cos(2α﹣120°)+cos2α+cos(2α+120°)]
= ![]() =右边.
=右边.
∴结论正确.
【解析】分析已知条件中:sin230°+sin290°+sin2150°= ![]() ,sin25°+sin265°+sin2125°=
,sin25°+sin265°+sin2125°= ![]() .我们可以发现等式左边参加累加的三个均为正弦的平方,且三个角组成一个以60°为公差的等差数列,右边是常数,由此不难得到结论.
.我们可以发现等式左边参加累加的三个均为正弦的平方,且三个角组成一个以60°为公差的等差数列,右边是常数,由此不难得到结论.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,ABCD﹣A1B1C1D1为正方体,下面结论错误的是( ) 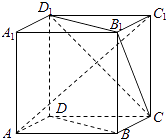
A.BD∥平面CB1D1
B.AC1⊥BD
C.异面直线AD与CB1角为60°
D.AC1⊥平面CB1D1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a,b为两条直线,α,β为两个平面,下列四个命题中,正确的命题是( )
A.若a,b与α所成的角相等,则α∥b
B.若a∥α,b∥β,α∥β,则a∥b
C.若aα,bβ,α∥b,则α∥β
D.若a⊥α,b⊥β,α⊥β,是a⊥b
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义运算: ![]() ;,例如23=3,则下列等式不能成立的是( )
;,例如23=3,则下列等式不能成立的是( )
A.ab=ba
B.(ab)c=a(bc)
C.(ab)2=a2b2
D.c(ab)=(ca)(cb)(c>0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】证明.
(1)用数学归纳法证明:12+22+32+…+n2= ![]() ,n是正整数;
,n是正整数;
(2)用数学归纳法证明不等式:1+ ![]() +
+ ![]() +…+
+…+ ![]() <2
<2 ![]() (n∈N*)
(n∈N*)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到如下数据:
(1)根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(2)根据表中数据,在调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50名的学生人数为X,求X的分布列和数学期望.
年级名次 | 1~50 | 951~1000 |
近视 | 41 | 32 |
不近视 | 9 | 18 |
附:P(K2≥3.841=0.05)K2= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=cos(ωx+φ)(ω>0,﹣ ![]() <φ<0)的最小正周期为π,且f(
<φ<0)的最小正周期为π,且f( ![]() )=
)= ![]() .
.
(1)求ω和φ的值;
(2)求f(x)的单调递增区间;
(3)求f(x)在[0, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com