
【题目】如图,在三棱柱![]() 中,侧面
中,侧面![]() 是菱形,
是菱形,![]() ,
,![]() .
.
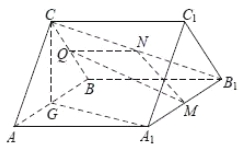
(1)若![]() 是线段
是线段![]() 的中点,求证:平面
的中点,求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 、
、![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 、
、![]() 的中点,求证:直线
的中点,求证:直线![]() 平面
平面![]() .
.
科目:高中数学 来源: 题型:
【题目】“垛积术”(隙积术)是由北宋科学家沈括在《梦溪笔谈》中首创,南宋数学家杨辉、元代数学家朱世杰丰富和发展的一类数列求和方法,有菱草垛、方垛、刍童垛、三角垛等等,某仓库中部分货物堆放成如图所示的“菱草垛”:自上而下,第一层1件,以后每一层比上一层多1件,最后一层是n件,已知第一层货物单价1万元,从第二层起,货物的单价是上一层单价的![]() .若这堆货物总价是
.若这堆货物总价是![]() 万元,则n的值为( )
万元,则n的值为( )
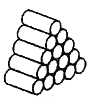
A. 7B. 8C. 9D. 10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电子计算机诞生于20世纪中叶,是人类最伟大的技术发明之一.计算机利用二进制存储信息,其中最基本单位是“位(bit)”,1位只能存放2种不同的信息:0或l,分别通过电路的断或通实现.“字节(Byte)”是更大的存储单位,1Byte=8bit,因此1字节可存放从00000000(2)至11111111(2)共256种不同的信息.将这256个二进制数中,所有恰有相邻两位数是1其余各位数均是0的所有数相加,则计算结果用十进制表示为
A. 254B. 381C. 510D. 765
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
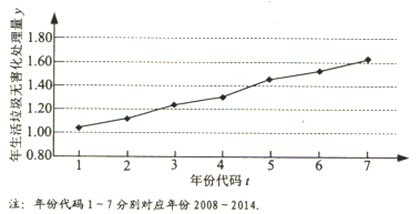
(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据:![]() ,
,![]() ,
,
![]() ,
,![]() ≈2.646.
≈2.646.
参考公式:相关系数
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() 的底面边长和侧棱长都为2,
的底面边长和侧棱长都为2,![]() 是
是![]() 的中点.
的中点.
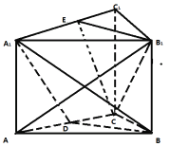
(1)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 平面
平面![]() ,若存在指出点
,若存在指出点![]() 在线段
在线段![]() 上的位置,若不存在,请说明理由;
上的位置,若不存在,请说明理由;
(2)求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.

(Ⅰ)求这些产品质量指标值落在区间![]() 内的频率;
内的频率;
(Ⅱ)用分层抽样的方法在区间![]() 内抽取一个容量为6的样本,将该样本看成一个总体,从中任意
内抽取一个容量为6的样本,将该样本看成一个总体,从中任意
抽取2件产品,求这2件产品都在区间![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com