
【题目】已知![]() .
.
(Ⅰ)当![]() 时,判断
时,判断![]() 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)若![]() 在
在![]() 上的最小值为
上的最小值为![]() ,求
,求![]() 的值.
的值.
【答案】(1)f(x)在(0,+∞)上是单调递增函数
(2)a=-![]() .
.
【解析】
试题分析:(1)利用导数判定函数单调性:先求导数f ′(x)=![]() +
+![]() =
=![]() .因为定义域为(0,+∞),a>0 所以f ′(x)>0,故f(x)在(0,+∞)上是单调递增函数.(2)先分类确定f(x)在[1,e]上的最小值:①若a≥-1,f ′(x)≥0,f(x)在[1,e]上为增函数,f(x)min=f(1)=-a=
.因为定义域为(0,+∞),a>0 所以f ′(x)>0,故f(x)在(0,+∞)上是单调递增函数.(2)先分类确定f(x)在[1,e]上的最小值:①若a≥-1,f ′(x)≥0,f(x)在[1,e]上为增函数,f(x)min=f(1)=-a=![]() ,∴a=-
,∴a=-![]() (舍去).若a≤-e,f ′(x)≤0, f(x)在[1,e]上为减函数,f(x)min=f(e)=1-
(舍去).若a≤-e,f ′(x)≤0, f(x)在[1,e]上为减函数,f(x)min=f(e)=1-![]() =
=![]() ,∴a=-
,∴a=-![]() (舍去).若-e<a<-1,令f ′(x)=0,得x=-a. f(x)min=f(-a)=ln(-a)+1=
(舍去).若-e<a<-1,令f ′(x)=0,得x=-a. f(x)min=f(-a)=ln(-a)+1=![]() a=-
a=-![]() .
.
试题解析:解:(1)由题得f(x)的定义域为(0,+∞),且 f ′(x)=![]() +
+![]() =
=![]() .
.
∵a>0,∴f ′(x)>0,故f(x)在(0,+∞)上是单调递增函数. 3’
(2)由(1)可知:f ′(x)=![]() ,
,
①若a≥-1,则x+a≥0,即f ′(x)≥0在[1,e]上恒成立,此时f(x)在[1,e]上为增函数,
∴f(x)min=f(1)=-a=![]() ,∴a=-
,∴a=-![]() (舍去).
(舍去).
②若a≤-e,则x+a≤0,即f ′(x)≤0在[1,e]上恒成立,此时f(x)在[1,e]上为减函数,
∴f(x)min=f(e)=1-![]() =
=![]() ,∴a=-
,∴a=-![]() (舍去).
(舍去).
③若-e<a<-1,令f′(x)=0,得x=-a.
当1<x<-a时,f ′(x)<0,∴f(x)在(1,-a)上为减函数;
当-a<x<e时,f ′(x)>0,∴f(x)在(-a,e)上为增函数,
∴f(x)min=f(-a)=ln(-a)+1=![]() a=-
a=-![]() .
.
综上可知:a=-![]() . 12’
. 12’


科目:高中数学 来源: 题型:
【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在
,分数在![]() 以上(含
以上(含![]() )的同学获奖. 按文理科用分层抽样的方法抽取
)的同学获奖. 按文理科用分层抽样的方法抽取![]() 人的成绩作为样本,得到成绩的频率分布直方图(见下图).
人的成绩作为样本,得到成绩的频率分布直方图(见下图).
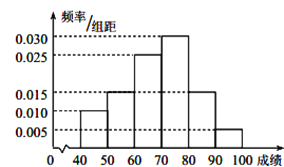
(I)在答题卡上填写下面的![]() 列联表,能否有超过
列联表,能否有超过![]() 的把握认为“获奖与学生的文理科有关”?
的把握认为“获奖与学生的文理科有关”?
文科生 | 理科生 | 合计 | |
获奖 |
| ||
不获奖 | |||
合计 |
|
(II)将上述调査所得的频率视为概率,现从该校参与竞赛的学生中,任意抽取![]() 名学生,记“获奖”学生人数为
名学生,记“获奖”学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表及公式:,其中
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某人做某件事,成功的概率只有0.1.用计算器计算,如果他尝试10次,而且每次是否成功都相互独立,则他至少有一次成功的概率为多少(精确到0.01)?如果他尝试20次呢?如果要保证至少成功一次的概率不小于90%,则他至少要尝试多少次?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在本校任选了一个班级,对全班50名学生进行了作业量的调查,根据调查结果统计后,得到如下的![]() 列联表,已知在这50人中随机抽取2人,这2人都“认为作业量大”的概率为
列联表,已知在这50人中随机抽取2人,这2人都“认为作业量大”的概率为![]() .
.
认为作业量大 | 认为作业量不大 | 合计 | |
男生 | 18 | ||
女生 | 17 | ||
合计 | 50 |
(1)请完成上面的列联表;
(2)根据列联表的数据,能否有![]() 的把握认为“认为作业量大”与“性别”有关?
的把握认为“认为作业量大”与“性别”有关?
附表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
附: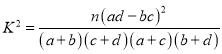 (其中
(其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地某路无人驾驶公交车发车时间间隔![]() (单位:分钟)满足
(单位:分钟)满足![]() ,
,![]() .经测算,该路无人驾驶公交车载客量
.经测算,该路无人驾驶公交车载客量![]() 与发车时间间隔
与发车时间间隔![]() 满足:
满足: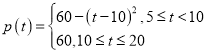 ,其中
,其中![]() .
.
(1)求![]() ,并说明
,并说明![]() 的实际意义;
的实际意义;
(2)若该路公交车每分钟的净收益![]() (元),问当发车时间间隔为多少时,该路公交车每分钟的净收益最大?并求每分钟的最大净收益.
(元),问当发车时间间隔为多少时,该路公交车每分钟的净收益最大?并求每分钟的最大净收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代儒家要求学生掌握六种基本才艺:礼、乐、射、御、书、数,简称“六艺”,某高中学校为弘扬“六艺”的传统文化,分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识竞赛,现有甲、乙、丙三位选手进入了前三名的最后角逐,规定:每场知识竞赛前三名的得分都分别为![]()
![]() 且
且![]() ;选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为
;选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为![]() 分,乙和丙最后得分都是
分,乙和丙最后得分都是![]() 分,且乙在其中一场比赛中获得第一名,下列说法正确的是( )
分,且乙在其中一场比赛中获得第一名,下列说法正确的是( )
A. 乙有四场比赛获得第三名
B. 每场比赛第一名得分![]() 为
为![]()
C. 甲可能有一场比赛获得第二名
D. 丙可能有一场比赛获得第一名
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,平行四边形OABC,顶点O,A,C分别表示0,3+2i,-2+4i,试求:
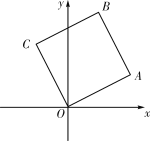
(1) ![]() 所表示的复数;
所表示的复数;
(2)对角线![]() 所表示的复数;
所表示的复数;
(3)B点对应的复数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com