Question

【题目】已知函数 若方程恰有三个实数根，则实数的取值范围是_______.

Answer 1

【答案】

【解析】

令f（t）＝2，解出t，则f（x）＝t，讨论k的符号，根据f（x）的函数图象得出t的范围即可．

解：令f（t）＝2得t＝﹣1或t（k≠0）．

∵f（f（x））﹣2＝0，∴f（f（x））＝2，

∴f（x）＝﹣1或f（x）（k≠0）．

（1）当k＝0时，做出f（x）的函数图象如图所示：

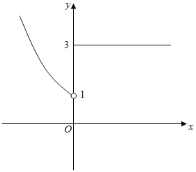
由图象可知f（x）＝﹣1无解，即f（f（x））﹣2＝0无解，不符合题意；

（2）当k＞0时，做出f（x）的函数图象如图所示：

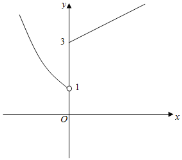
由图象可知f（x）＝﹣1无解，f（x）无解，即f（f（x））﹣2＝0无解，不符合题意；

（3）当k＜0时，做出f（x）的函数图象如图所示：

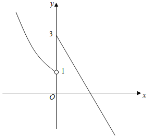
由图象可知f（x）＝﹣1有1解，

∵f（f（x））﹣2＝0有3解，∴f（x）有2解，

∴1，解得﹣1＜k．

综上，k的取值范围是（﹣1，]．

故答案为：（﹣1，]