
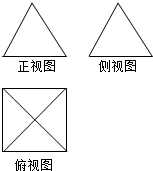
 若一个四梭锥的三视图如图所示,其中正视图与侧视图都是边长为2的等边三角形,则该四棱锥的四条侧棱长之和等于4$\sqrt{5}$.
若一个四梭锥的三视图如图所示,其中正视图与侧视图都是边长为2的等边三角形,则该四棱锥的四条侧棱长之和等于4$\sqrt{5}$. 分析 根据几何体的三视图,得出该几何体是底面边长为2的正四棱锥,求出高即可求出侧棱长.
解答 解:根据几何体的三视图,得;
该几何体是底面边长为2的正四棱锥,
且正四棱锥的高是$\sqrt{{2}^{2}{-(\frac{2}{2})}^{2}}$=$\sqrt{3}$;
所以它的四条侧棱长相等,为$\sqrt{{(\sqrt{3})}^{2}{+(\frac{2\sqrt{2}}{2})}^{2}}$=$\sqrt{5}$;
所以,四条侧棱长之和为4$\sqrt{5}$.
故答案为:4$\sqrt{5}$.
点评 本题考查了空间几何体三视图的应用问题,也考查了空间想象能力的应用问题,是基础题目.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 至少有一个白球;都是白球 | B. | 至少有一个白球;至少有一个红球 | ||
| C. | 至少有一个白球;红球、黑球各一个 | D. | 恰有一个白球;白球、黑球各一个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校决定为本校上学时间不少于30分钟的学生提供校车接送服务.为了解学生上学所需时间,从全校600名学生中抽取50人统计上学时间(单位:分钟),现对600人随机编号为001,002,…600.抽取50位学生上学时间均不超过60分钟,将时间按如下方式分成六组,第一组上学时间在[0,10),第二组上学时间在[10,20),…第六组上学时间在[50,60]得到各组人数的频率分布直方图.如图.
某校决定为本校上学时间不少于30分钟的学生提供校车接送服务.为了解学生上学所需时间,从全校600名学生中抽取50人统计上学时间(单位:分钟),现对600人随机编号为001,002,…600.抽取50位学生上学时间均不超过60分钟,将时间按如下方式分成六组,第一组上学时间在[0,10),第二组上学时间在[10,20),…第六组上学时间在[50,60]得到各组人数的频率分布直方图.如图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b<-1或b>1 | B. | -1<b<1 | C. | b>1 | D. | b>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com