
分析 (1)在函数y=f(x)的图象任取一点P(x,y),由已知式子证明点P关于直线x=2的对称点P′(4-x,y)也在函数图象上;
(2)可证函数f(x)是周期为4的周期函数,由周期性和对称性可得分段函数的解析式.
解答 (1)证明:在函数y=f(x)的图象任取一点P(x,y),
则点P关于直线x=2的对称点P′(4-x,y),
∵对一切实数x,都满足f(2+x)=f(2-x),
∴f(x)=f[2-(x-2)]=f(4-x)
∴y=f(4-x)=f(x),即P′也在函数图象上,
∴函数y=f(x)的图象关于直线x=2对称;
(2)由(1)知,任意x都有f(4-x)=f(x),
又f(x)是偶函数,∴f(x-4)=f(x),
∴函数f(x)是周期为4的周期函数,
当x∈[-4,-2],∴x+4∈[0,2],
又x∈[0,2]时,f(x)=2x-1,
∴当x∈[-4,-2]时,f(x+4)=2(x+4)-1=2x+7,
∴此时函数的解析为f(x)=2x+7;
又函数f(x)的图象关于直线x=2对称,也关于x=-2对称,
由对称性可知当x∈(-2,0]时函数f(x)的图象为线段,
且经过点(-2,3)和(0,-1),
∴当x∈(-2,0]时,函数的解析为f(x)=-2x-1,
∴x∈[-4,0]时函数f(x)的解析式为f(x)=$\left\{\begin{array}{l}{2x+7,x∈[-4,-2]}\\{-2x-1,x∈(-2,0]}\end{array}\right.$
点评 本题考查抽象函数的对称性和周期性,涉及分段函数解析式的求解和直线方程,属中档题.


科目:高中数学 来源: 题型:解答题
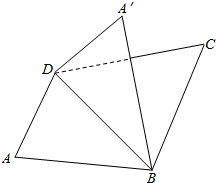 已知ABCD是直角梯形,AB=AD,AD∥BC,AB⊥BC,CD⊥BD,把△ABD沿BD折起,使平面A′BD⊥面BCD.
已知ABCD是直角梯形,AB=AD,AD∥BC,AB⊥BC,CD⊥BD,把△ABD沿BD折起,使平面A′BD⊥面BCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
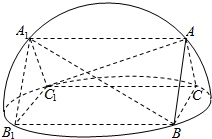 如图,侧棱垂直于底面的三棱柱ABC-A1B1C1的六个顶点都在一个半球面上,且AB=AC,B1C1=$\sqrt{2}$BB1,则异面直线AC1与A1B所成的角为( )
如图,侧棱垂直于底面的三棱柱ABC-A1B1C1的六个顶点都在一个半球面上,且AB=AC,B1C1=$\sqrt{2}$BB1,则异面直线AC1与A1B所成的角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com