
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() ,试判断
,试判断![]() 的零点个数.
的零点个数.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上是增函数,
上是增函数,
当![]() ,
,![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
当![]() 时,
时,![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,在
上是减函数,在![]() 上是增函数;
上是增函数;
(2)1
【解析】
(1)对![]() 求导后对
求导后对![]() 进行分类讨论,找到
进行分类讨论,找到![]() 和
和![]() 的区间,即为
的区间,即为![]() 的单调区间.
的单调区间.
(2)由(1)可知![]() 时,
时,![]() 有极大值
有极大值![]() 和极小值
和极小值![]() ,研究他们的正负,并且找到令
,研究他们的正负,并且找到令![]() 的点,根据零点存在定理,找出零点个数.
的点,根据零点存在定理,找出零点个数.
(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() ,令
,令![]() ,则
,则![]() ,
,![]() ,
,
(i)若![]() ,则
,则![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上是增函数,
上是增函数,
(ii)若![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 是增函数,
是增函数,
当![]() 时,
时,![]() ,
,![]() 是减函数,
是减函数,
当![]() 时,
时,![]() ,
,![]() 是增函数,
是增函数,
(iii)若![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 是增函数,
是增函数,
当![]() 时,
时,![]() ,
,![]() 是减函数,
是减函数,
当![]() 时,
时,![]() ,
,![]() 是增函数,
是增函数,
综上所述:当![]() 时,
时,![]() 在
在![]() 上是增函数,
上是增函数,
当![]() ,
,![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
当![]() 时,
时,![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,在
上是减函数,在![]() 上是增函数;
上是增函数;
(2)当![]() 时,
时,
![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
所以![]() 的极小值为
的极小值为![]() ,
,
![]() 的极大值为
的极大值为![]() ,
,
设![]() ,其中
,其中![]() ,
,
![]() ,
,
所以![]() 在
在![]() 上是增函数,
上是增函数,
所以![]() ,
,
因为![]() ,
,
所以有且仅有1个![]() ,使
,使![]() .
.
所以当![]() 时,
时,![]() 有且仅有1个零点.
有且仅有1个零点.


科目:高中数学 来源: 题型:
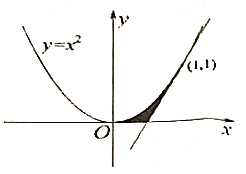
【题目】我国南北朝时期的数学家祖暅提出了计算体积的祖暅原理:“幂势既同,则积不容异。”意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.已知曲线![]() ,直线
,直线![]() 为曲线
为曲线![]() 在点
在点![]() 处的切线.如图所示,阴影部分为曲线
处的切线.如图所示,阴影部分为曲线![]() 、直线
、直线![]() 以及
以及![]() 轴所围成的平面图形,记该平面图形绕
轴所围成的平面图形,记该平面图形绕![]() 轴旋转一周所得的几何体为
轴旋转一周所得的几何体为![]() .给出以下四个几何体:
.给出以下四个几何体:





① ② ③ ④
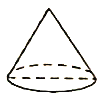
图①是底面直径和高均为![]() 的圆锥;
的圆锥;
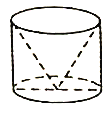
图②是将底面直径和高均为![]() 的圆柱挖掉一个与圆柱同底等高的倒置圆锥得到的几何体;
的圆柱挖掉一个与圆柱同底等高的倒置圆锥得到的几何体;
图③是底面边长和高均为![]() 的正四棱锥;
的正四棱锥;
图④是将上底面直径为![]() ,下底面直径为
,下底面直径为![]() ,高为
,高为![]() 的圆台挖掉一个底面直径为
的圆台挖掉一个底面直径为![]() ,高为
,高为![]() 的倒置圆锥得到的几何体.
的倒置圆锥得到的几何体.
根据祖暅原理,以上四个几何体中与![]() 的体积相等的是( )
的体积相等的是( )
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学的高二(1)班男同学![]() 名,女同学
名,女同学![]() 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个![]() 人的课外兴趣小组.
人的课外兴趣小组.
(1)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;
(2)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出![]() 名同学做实验,该同学做完后,再从小组内剩下的同学中选
名同学做实验,该同学做完后,再从小组内剩下的同学中选![]() 名同学做实验,求选出的两名同学中恰有
名同学做实验,求选出的两名同学中恰有![]() 名女同学的概率;
名女同学的概率;
(3)实验结束后,第一次做实验的同学得到的实验数据为![]() ,第二次做实验的同学得到的实验数据为
,第二次做实验的同学得到的实验数据为![]() ,请问哪位同学的实验更稳定?并说明理由.
,请问哪位同学的实验更稳定?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的有________(填序号)
①已知![]() 或
或![]() ,
,![]() ,则p是q的充分不必要条件;
,则p是q的充分不必要条件;
②“函数![]() 的最小正周期为
的最小正周期为![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
③![]() 中,内角A,B,C所对的边分别为a,b,c,
中,内角A,B,C所对的边分别为a,b,c,![]() ,
,![]() ,则“
,则“![]() ”是“
”是“![]() 为等腰三角形”的必要不充分条件;
为等腰三角形”的必要不充分条件;
④若命题![]() “函数
“函数![]() 的值域为
的值域为![]() ”为真命题,则实数a的取值范围是
”为真命题,则实数a的取值范围是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南北朝时期的数学家祖暅提出了计算体积的祖暅原理:“幂势既同,则积不容异。”意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.已知曲线![]() ,直线
,直线![]() 为曲线
为曲线![]() 在点
在点![]() 处的切线.如图所示,阴影部分为曲线
处的切线.如图所示,阴影部分为曲线![]() 、直线
、直线![]() 以及
以及![]() 轴所围成的平面图形,记该平面图形绕
轴所围成的平面图形,记该平面图形绕![]() 轴旋转一周所得的几何体为
轴旋转一周所得的几何体为![]() .给出以下四个几何体:
.给出以下四个几何体:


① ② ③ ④
图①是底面直径和高均为![]() 的圆锥;
的圆锥;
图②是将底面直径和高均为![]() 的圆柱挖掉一个与圆柱同底等高的倒置圆锥得到的几何体;
的圆柱挖掉一个与圆柱同底等高的倒置圆锥得到的几何体;
图③是底面边长和高均为![]() 的正四棱锥;
的正四棱锥;
图④是将上底面直径为![]() ,下底面直径为
,下底面直径为![]() ,高为
,高为![]() 的圆台挖掉一个底面直径为
的圆台挖掉一个底面直径为![]() ,高为
,高为![]() 的倒置圆锥得到的几何体.
的倒置圆锥得到的几何体.
根据祖暅原理,以上四个几何体中与![]() 的体积相等的是( )
的体积相等的是( )
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:关于x的方程x![]() a在(1,+∞)上有实根;命题q:方程
a在(1,+∞)上有实根;命题q:方程![]() 1表示的曲线是焦点在x轴上的椭圆.
1表示的曲线是焦点在x轴上的椭圆.
(1)若p是真命题,求a的取值范围;
(2)若p∧q是真命题,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com