[题目]田忌和齐王赛马是历史上有名的故事,设齐王的三匹马分别为A1,A2,A3;田忌的三匹马分别为B1,B2,B3;三匹马各比赛一次,胜两场者获胜,双方均不知对方的马出场顺序.(1)若这六匹马比赛优.劣程度可以用不等式表示:A1>B1>A2>B2>A3>B3,则田忌获胜的概率是多大?(2)若这六匹马比赛优.劣程度可以用不等式表示:A1& 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】田忌和齐王赛马是历史上有名的故事,设齐王的三匹马分别为A1,A2,A3;田忌的三匹马分别为B1,B2,B3;三匹马各比赛一次,胜两场者获胜,双方均不知对方的马出场顺序.

(1)若这六匹马比赛优、劣程度可以用不等式表示:A1>B1>A2>B2>A3>B3,则田忌获胜的概率是多大?

(2)若这六匹马比赛优、劣程度可以用不等式表示:A1>B1>A2>B2>B3>A3,则田忌获胜的概率是多大?

【答案】(1) (2)

【解析】试题分析：列出齐王与田忌赛马的所有情况，利用古典概型求概率即可.

试题解析：

不妨设齐王的三匹马出场次序定为A1A2A3,则田忌的马出场次序的基本事件空间:{B1B2B3,B1B3B2,B2B1B3,B2B3B1,B3B1B2,B3B2B1}.

(1)田忌赢齐王的三匹马的出场次序为B3B1B2,则田忌获胜的概率是.

(2)田忌赢齐王的三匹马的出场次序为B3B1B2,B2B1B3,则田忌获胜的概率是.

练习册系列答案

绿色互动空间阶梯调研测试系列答案

课本配套练习系列答案

应用题天天练东北师范大学出版社系列答案

应用题天天练四川大学出版社系列答案

全国中考试题分类精选系列答案

初中学业考试指导系列答案

练习册吉林出版集团有限责任公司系列答案

英语同步听力系列答案

初中英语听力系列答案

单元测试卷齐鲁书社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】某同学用“描点法”画函数在区间上的图象时,列表并填入了部分数据,如下表：

(1)请将上表数据补充完整,并在给出的直角坐标系中,画出在区间上的图象；

(2)利用函数的图象,直接写出函数在上的单调递增区间；

(3)将图象上所有点向左平移个单位长度,得到的图象,若

图象的一个对称中心为,求的最小值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在三棱锥V-ABC中，平面VAB平面ABC， VAB为等边三角形，ACBC且AC=BC=，O,M分别为AB,VA的中点。

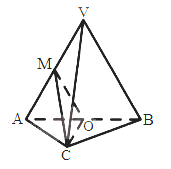
（I）求证：VB//平面MOC；

（II）求证：平面MOC平面VAB；

（III）求三棱锥V-ABC的体积。

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】定义在R上的奇函数f（x）满足f（x﹣2）=f（x+2），且当x∈[﹣2，0]时，f（x）=3x﹣1，则f（9）=（）
A.﹣2
B.2
C.
D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在无穷数列中，，对于任意，都有，，设，记使得成立的的最大值为．

（）设数列为，，，，，写出，，的值．

（）若为等比数列，且，求的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某教育机构随机抽查某校20个班级,调查各班关注汉字听写大赛的学生人数,根据所得数据的茎叶图,以5为组距将数据分组成[0,5),[5,10),[10,15),[15,20),[20,25),[25,30),[30,35),[35,40]时,所作的频率分布直方图如图所示,则原始茎叶图可能是(　　)