
【题目】已知![]() ,
,![]() ,其中实数
,其中实数![]() .
.
(1)求![]() 的最大值;
的最大值;
(2)若![]() 对于任意实数
对于任意实数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按200元/次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如下:
消费次第 | 第1次 | 第2次 | 第3次 | 第4次 | ≥5次 |
收费比率 | 1 | 0.95 | 0.90 | 0.85 | 0.80 |
该公司注册的会员中没有消费超过5次的,从注册的会员中,随机抽取了100位进行统计,得到统计数据
如下:
消费次数 | 1次 | 2次 | 3次 | 4次 | 5次 |
人数 | 60 | 20 | 10 | 5 | 5 |
假设汽车美容一次,公司成本为150元,根据所给数据,解答下列问题:
(1)某会员仅消费两次,求这两次消费中,公司获得的平均利润;
(2)以事件发生的频率作为相应事件发生的概率, 设该公司为一位会员服务的平均利润为![]() 元,求
元,求![]() 大于40的概率.
大于40的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图甲,AD,BC是等腰梯形CDEF的两条高,![]() ,点M是线段AE的中点,将该等腰梯形沿着两条高AD,BC折叠成如图乙所示的四棱锥P-ABCD(E,F重合,记为点P).
,点M是线段AE的中点,将该等腰梯形沿着两条高AD,BC折叠成如图乙所示的四棱锥P-ABCD(E,F重合,记为点P).
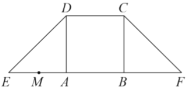
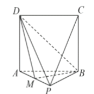
甲 乙
(1)求证:![]() ;
;
(2)求点M到平面BDP距离h.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为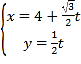 (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)在曲线![]() 上任取一点
上任取一点![]() ,连接
,连接![]() ,在射线
,在射线![]() 上取一点
上取一点![]() ,使
,使![]() ,求
,求![]() 点轨迹的极坐标方程;
点轨迹的极坐标方程;
(2)在曲线![]() 上任取一点
上任取一点![]() ,在曲线
,在曲线![]() 上任取一点
上任取一点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年
年![]() 月,中国良渚古城遗址获准列入世界遗产名录,标志着中华五千年文明史得到国际社会认可.良渚古城遗址是人类早期城市文明的范例,实证了中华五千年文明史.考古科学家在测定遗址年龄的过程中利用了“放射性物质因衰变而减少”这一规律.已知样本中碳
月,中国良渚古城遗址获准列入世界遗产名录,标志着中华五千年文明史得到国际社会认可.良渚古城遗址是人类早期城市文明的范例,实证了中华五千年文明史.考古科学家在测定遗址年龄的过程中利用了“放射性物质因衰变而减少”这一规律.已知样本中碳![]() 的质量
的质量![]() 随时间
随时间![]() (单位:年)的衰变规律满足
(单位:年)的衰变规律满足![]() (
(![]() 表示碳
表示碳![]() 原有的质量),则经过
原有的质量),则经过![]() 年后,碳
年后,碳![]() 的质量变为原来的________;经过测定,良渚古城遗址文物样本中碳
的质量变为原来的________;经过测定,良渚古城遗址文物样本中碳![]() 的质量是原来的
的质量是原来的![]() 至
至![]() ,据此推测良渚古城存在的时期距今约在________年到
,据此推测良渚古城存在的时期距今约在________年到![]() 年之间.(参考数据:
年之间.(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题:
①“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
②“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 上为增函数”的充分不必要条件
上为增函数”的充分不必要条件
③若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为假命题
均为假命题
④对于命题![]() :
:![]() ,
,![]() ,则
,则![]() 为:
为:![]() ,
,![]()
其中真命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com