
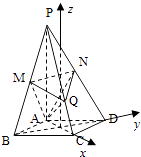
【题目】如图,在四棱锥P﹣ABCD中,底面是边长为 ![]() 的菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2
的菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2 ![]() ,M,N分别为PB,PD的中点.
,M,N分别为PB,PD的中点. 
(1)证明:MN∥平面ABCD;
(2)过点A作AQ⊥PC,垂足为点Q,求二面角A﹣MN﹣Q的平面角的余弦值.
【答案】
(1)证明:连接BD.∵M,N分别为PB,PD的中点,
∴在△PBD中,MN∥BD.
又MN平面ABCD,BD平面ABCD
∴MN∥平面ABCD
(2)方法一:连接AC交BD于O,以O为原点,OC,OD所在直线为x,y轴,建立空间直角坐标系,在菱形ABCD中,∠BAD=120°
,得AC=AB= ![]() ,BD=
,BD= ![]()
∵PA⊥平面ABCD,∴PA⊥AC
在直角△PAC中, ![]() ,AQ⊥PC得QC=2,PQ=4,由此知各点坐标如下
,AQ⊥PC得QC=2,PQ=4,由此知各点坐标如下
A(﹣ ![]() ,0,0),B(0,﹣3,0),C(
,0,0),B(0,﹣3,0),C( ![]() ,0,0),D(0,3,0),P(
,0,0),D(0,3,0),P( ![]() ),M(
),M( ![]() ),N(
),N( ![]() )
)
Q( ![]() )
)
设 ![]() =(x,y,z)为平面AMN的法向量,则
=(x,y,z)为平面AMN的法向量,则 ![]() .
.
∴ 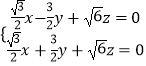 ,取z=﹣1,
,取z=﹣1, ![]() ,
,
同理平面QMN的法向量为 ![]()
∴ 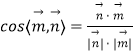 =
= ![]()
∴所求二面角A﹣MN﹣Q的平面角的余弦值为 ![]() .
.
方法二:在菱形ABCD中,∠BAD=120°,得AC=AB=BC=CD=DA= ![]() ,BD=
,BD= ![]()
∵PA⊥平面ABCD,∴PA⊥AB,PA⊥AC,PA⊥AD,∴PB=PC=PD,∴△PBC≌△PDC
而M,N分别是PB,PD的中点,∴MQ=NQ,且AM= ![]() PB=
PB= ![]() =AN
=AN
取MN的中点E,连接AE,EQ,则AE⊥MN,QE⊥MN,所以∠AEQ为二面角A﹣MN﹣Q的平面角
由 ![]() ,AM=AN=3,MN=3可得AE=
,AM=AN=3,MN=3可得AE= ![]()
在直角△PAC中,AQ⊥PC得QC=2,PQ=4,AQ=2 ![]()
在△PBC中,cos∠BPC= ![]()
在等腰△MQN中,MQ=NQ= ![]() .MN=3,∴QE=
.MN=3,∴QE= ![]()
在△AED中,AE= ![]() ,QE=
,QE= ![]() ,AQ=2
,AQ=2 ![]() ,∴cos∠AEQ=
,∴cos∠AEQ= ![]()
∴所求二面角A﹣MN﹣Q的平面角的余弦值为 ![]() .
.
【解析】(1)连接BD,利用三角形的中位线的性质,证明MN∥BD,再利用线面平行的判定定理,可知MN∥平面ABCD;(2)方法一:连接AC交BD于O,以O为原点,OC,OD所在直线为x,y轴,建立空间直角坐标系,求出平面AMN的法向量 ![]() ,利用向量的夹角公式,即可求得二面角A﹣MN﹣Q的平面角的余弦值;
,利用向量的夹角公式,即可求得二面角A﹣MN﹣Q的平面角的余弦值;
方法二:证明∠AEQ为二面角A﹣MN﹣Q的平面角,在△AED中,求得AE= ![]() ,QE=
,QE= ![]() ,AQ=2
,AQ=2 ![]() ,再利用余弦定理,即可求得二面角A﹣MN﹣Q的平面角的余弦值.
,再利用余弦定理,即可求得二面角A﹣MN﹣Q的平面角的余弦值.
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PD⊥平面ABCD,![]() ,∠ABC=∠BCD=90°,E为PB的中点。
,∠ABC=∠BCD=90°,E为PB的中点。

(1)证明:CE∥面PAD.
(2)若直线CE与底面ABCD所成的角为45°,求四棱锥P-ABCD的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列![]() 的前n项和.
的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老人,结果如下:
(Ⅰ)估计该地区老年人中,需要志愿提供帮助的老年人的比例;
(Ⅱ)能否有99℅的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(Ⅲ)根据(Ⅱ)的结论,能否提出更好的调查办法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由。
是否需要志愿者 性别 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
参考数据:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司在甲、乙两地同时销售一种品牌车,利润(单位:万元)分别为L1=-x2+21x和L2=2x,其中销售量为x(单位:辆).若该公司在两地共销售15辆,则能获得的最大利润为()
A. 90万元B. 120万元
C. 120.25万元D. 60万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区有小学150所,中学75所,大学25所.先采用分层抽样的方法从这些学校中抽取30所学校对学生进行视力调查,应从小学中抽取 18 所学校,中学中抽取所学校.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一项抛掷骰子的过关游戏规定:在第![]() 关要抛掷一颗骰子
关要抛掷一颗骰子![]() 次,如里这
次,如里这![]() 次抛掷所出现的点数和大于
次抛掷所出现的点数和大于![]() ,则算过关,可以随意挑战某一关.若直接挑战第三关,则通关的概率为______;若直接挑战第四关,则通关的慨率为______.
,则算过关,可以随意挑战某一关.若直接挑战第三关,则通关的概率为______;若直接挑战第四关,则通关的慨率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 经过点
经过点![]() ,且点
,且点![]() 到椭圆的两焦点的距离之和为
到椭圆的两焦点的距离之和为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 是椭圆
是椭圆![]() 上的两个点,线段
上的两个点,线段![]() 的中垂线
的中垂线![]() 的斜率为
的斜率为![]() 且直线
且直线![]() 与
与![]() 交于点
交于点![]() ,
,![]() 为坐标原点,求证:
为坐标原点,求证:![]() 三点共线.
三点共线.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com