
 如图:Rt△ABC中,∠ABC=90°,AB=BC.以AB为直径的⊙O交OC于D,AD的延长线交BC于E,过点D作⊙O的切线DF交BC于F,连OF.⊙C切⊙O于点D,交BC于G.
如图:Rt△ABC中,∠ABC=90°,AB=BC.以AB为直径的⊙O交OC于D,AD的延长线交BC于E,过点D作⊙O的切线DF交BC于F,连OF.⊙C切⊙O于点D,交BC于G.分析 (1)易证RT△OFD≌RT△OFB(HL),由全等三角形的性质可得∠FOD=∠FOB,又因为OA=OD,所以∠OAD=∠ODA,再由∠BOD=∠OAD+∠ODA=2∠OAD,可得∠FOB=∠OAD,进而可证明OF∥AE;
(2)连接BD交OF于H,易证AB2=AE•AD,BE2=DE•AE,再由三角形性质可得DF:CD=OB:BC=1:2,进而可求出DF,BE的值,由DE:AD=BE2:AB2计算即可.
解答 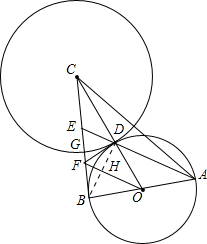 (1)证明:
(1)证明:
∵DF为⊙O的切线,
∴OD⊥DF,
∴∠FDO=90°
又∵∠ABC=90°,OD=OB,OF=OF,
∴在RT△OFD和RT△OFB中,OD=OB,OF=OF,
∴RT△OFD≌RT△OFB(HL),
∴∠FOD=∠FOB,
∵OA=OD,
∴∠OAD=∠ODA,
又∵∠BOD=∠OAD+∠ODA=2∠OAD,
∴∠FOB=∠OAD,
∴OF∥AE.
(2)解:连接BD交OF于H,
∵AB是直径,
∴BD⊥AE,
∴∠BDE=90°,
∵∠BAD=∠EAB,
∴△ABD∽△ABE,
∴AB2=AE•AD,
同理可证△BDE∽△ABE,
∴BE2=DE•AE,
∵∠FCD=∠OCB,∠CDF=∠CBO=90°,
∴△CDF∽△CBO,
∴DF:CD=OB:BC=1:2,
∴DF=$\frac{1}{2}$CD=$\frac{\sqrt{5}-1}{2}$R,
∵BC是⊙O的切线,
∴DF=BF,
∴DF是△BDE的中线,
∴BE=2DF=($\sqrt{5}$-1)R,
∴DE:AD=BE2:AB2=$\frac{3-\sqrt{5}}{2}$.
点评 本题考查了和圆有关的综合题目,用到的知识点有全等三角形的判定和性质、相似三角形的判定和性质、切线的性质、平行线的判定和性质以及等腰三角形的性质,题目的综合性较强,难度较大.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9-$\sqrt{2}$ | B. | 3+$\sqrt{2}$ | C. | 6-$\sqrt{2}$ | D. | 6+$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,O为坐标原点,A和B分别是椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1( a>b>0)和C2:$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{n}^{2}}$=1(m>n>0)上的动点,满足$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,且椭圆C2的离心率为$\frac{\sqrt{2}}{2}$.当动点A在x轴上的投影恰为C的右焦点F时,有S△AOF=$\frac{\sqrt{2}}{4}$
如图,O为坐标原点,A和B分别是椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1( a>b>0)和C2:$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{n}^{2}}$=1(m>n>0)上的动点,满足$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,且椭圆C2的离心率为$\frac{\sqrt{2}}{2}$.当动点A在x轴上的投影恰为C的右焦点F时,有S△AOF=$\frac{\sqrt{2}}{4}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 0 | 0.25 | 0.375 | 0.4065 | 0.438 |
| f(x) | -2 | -0.984 | -0.260 | -0.052 | -0.165 |
| x | 0.5 | 0.625 | 0.75 | 0.875 | 1 |
| f(x) | 0.625 | 1.982 | 2.645 | 4.35 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com