
 如图,三棱柱ADE-BCG中,四边形ABCD是矩形,F是EG的中点,EA⊥AB,AD=AE=EF=1,平面ABGE⊥平面ABCD.
如图,三棱柱ADE-BCG中,四边形ABCD是矩形,F是EG的中点,EA⊥AB,AD=AE=EF=1,平面ABGE⊥平面ABCD.分析 (1)推导出BC⊥AB,BC⊥AF,AF⊥BF,由此能证明AF⊥平面FBC.
(2)分别以AD、AB、AE所在直线为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出二面角B-FC-D的正弦值.
解答  证明:(1)∵四边形ABCD是矩形,∴BC⊥AB,
证明:(1)∵四边形ABCD是矩形,∴BC⊥AB,
又平面ABGE⊥平面ABCD,
∴BC⊥平面ABGE,
∵AF?平面ABGE,∴BC⊥AF,
在△AFB中,AF=BF=$\sqrt{2}$,AB=2,
∴AF2+BF2=AB2,即AF⊥BF,
∵BF∩BC=B,∴AF⊥平面FBC.
解:(2)分别以AD、AB、AE所在直线为x轴,y轴,z轴,建立空间直角坐标系,
则A(0,0,0),D(1,0,0),C(1,2,0),E(0,0,1),B(0,2,0),F(0,1,1),
∵$\overrightarrow{DC}$=(0,2,0),$\overrightarrow{DE}$=(-1,0,1),
设平面CDEF的一个法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DC}=2y=0}\\{\overrightarrow{n}•\overrightarrow{DE}=-x+z=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,0,1),
∵AF⊥平面FBC,∴平面FBC的一个法向量$\overrightarrow{AF}$=(0,1,1),
设二面角B-FC-D的平面角为θ,
则cosθ=$\frac{|\overrightarrow{n}•\overrightarrow{AF}|}{|\overrightarrow{n}|•|\overrightarrow{AF}|}$=$\frac{1}{2}$,
∴sinθ=$\sqrt{1-(\frac{1}{2})^{2}}$=$\frac{\sqrt{3}}{2}$.
∴二面角B-FC-D的正弦值是$\frac{\sqrt{3}}{2}$.
点评 本题考查线面垂直的证明,考查二面角的正弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是某校十大歌手比赛上,七位评委为某同学打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
如图是某校十大歌手比赛上,七位评委为某同学打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A. | 85,4.84 | B. | 85,1.6 | C. | 86,1.6 | D. | 86,4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
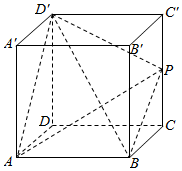 在棱长为4的正方体ABCD-A′B′C′D′中,点P在棱CC′上,且CC′=2CP.
在棱长为4的正方体ABCD-A′B′C′D′中,点P在棱CC′上,且CC′=2CP.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,ABCD是边长为2的菱形,且∠DAB=60°,PC=4,PA=2,E是PA的中点,平面PAC⊥平面ABCD.
如图,四棱锥P-ABCD中,ABCD是边长为2的菱形,且∠DAB=60°,PC=4,PA=2,E是PA的中点,平面PAC⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB,CD是圆O的两条互相垂直的直径,E是圆O上的点,过E点作圆O的切线交AB的延长线于F,连结CE交AB于G点.
如图,AB,CD是圆O的两条互相垂直的直径,E是圆O上的点,过E点作圆O的切线交AB的延长线于F,连结CE交AB于G点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com