
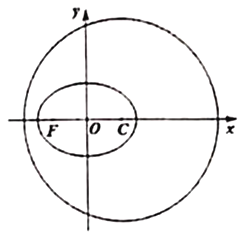
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)若直线![]() 过点
过点![]() ,且
,且![]() ,求
,求![]() 被椭圆
被椭圆![]() 所截得的弦的长度;
所截得的弦的长度;
(2)若已知点![]() 在椭圆
在椭圆![]() 上,动点
上,动点![]() 满足
满足![]() ,请判断点
,请判断点![]() 与圆
与圆![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,且椭圆过点
,且椭圆过点![]()
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 在椭圆
在椭圆![]() 上,
上,![]() 是坐标原点,若
是坐标原点,若![]() ,判定四边形
,判定四边形![]() 的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的偶函数
上的偶函数![]() 满足
满足![]() ,且
,且![]() ,当
,当![]() 时,
时,![]() .已知方程
.已知方程![]() 在区间
在区间![]() 上所有的实数根之和为
上所有的实数根之和为![]() .将函数
.将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,则
的图象,则![]() __________,
__________,![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某芯片公司对今年新开发的一批5G手机芯片进行测评,该公司随机调查了100颗芯片,并将所得统计数据分为![]() 五个小组(所调查的芯片得分均在
五个小组(所调查的芯片得分均在![]() 内),得到如图所示的频率分布直方图,其中
内),得到如图所示的频率分布直方图,其中![]() .
.
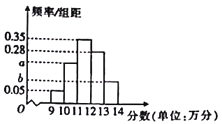
(1)求这100颗芯片评测分数的平均数(同一组中的每个数据可用该组区间的中点值代替).
(2)芯片公司另选100颗芯片交付给某手机公司进行测试,该手机公司将每颗芯片分别装在3个工程手机中进行初测。若3个工程手机的评分都达到11万分,则认定该芯片合格;若3个工程手机中只要有2个评分没达到11万分,则认定该芯片不合格;若3个工程手机中仅1个评分没有达到11万分,则将该芯片再分别置于另外2个工程手机中进行二测,二测时,2个工程手机的评分都达到11万分,则认定该芯片合格;2个工程手机中只要有1个评分没达到11万分,手机公司将认定该芯片不合格.已知每颗芯片在各次置于工程手机中的得分相互独立,并且芯片公司对芯片的评分方法及标准与手机公司对芯片的评分方法及标准都一致(以频率作为概率).每颗芯片置于一个工程手机中的测试费用均为300元,每颗芯片若被认定为合格或不合格,将不再进行后续测试,现手机公司测试部门预算的测试经费为10万元,试问预算经费是否足够测试完这100颗芯片?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4x+3sinx,x∈(-1,1),如果f(1-a)+f(1-a2)<0成立,则实数a的取值范围为( )
A. (0,1) B. ![]() C.
C. ![]() D. (-∞,-2)∪(1,+∞)
D. (-∞,-2)∪(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
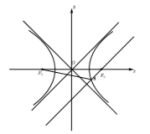
【题目】如图,已知双曲线![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,过右焦点作平行于一条渐近线的直线交双曲线于点
,过右焦点作平行于一条渐近线的直线交双曲线于点![]() ,若
,若![]() 的内切圆半径为
的内切圆半径为![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂加工某种零件需要经过![]() ,
,![]() ,
,![]() 三道工序,且每道工序的加工都相互独立,三道工序加工合格的概率分别为
三道工序,且每道工序的加工都相互独立,三道工序加工合格的概率分别为![]() ,
,![]() ,
,![]() .三道工序都合格的零件为一级品;恰有两道工序合格的零件为二级品;其它均为废品,且加工一个零件为二级品的概率为
.三道工序都合格的零件为一级品;恰有两道工序合格的零件为二级品;其它均为废品,且加工一个零件为二级品的概率为![]() .
.
(1)求![]() ;
;
(2)若该零件的一级品每个可获利200元,二级品每个可获利100元,每个废品将使工厂损失50元,设一个零件经过三道工序加工后最终获利为![]() 元,求
元,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是正方形,点
是正方形,点![]() 在以
在以![]() 为直径的半圆弧上(
为直径的半圆弧上(![]() 不与
不与![]() ,
,![]() 重合),
重合),![]() 为线段
为线段![]() 的中点,现将正方形
的中点,现将正方形![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.

(1)证明:![]() 平面
平面![]() .
.
(2)三棱锥![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com