
【题目】已知函数f(x)=ax+lnx(a∈R),g(x)=x2emx(m∈R,e为自然对数的底数).
(1)讨论函数f(x)的单调性及最值;
(2)若a>0,且对x1,x2∈[0,2],f(x1+1)≥g(x2)+a﹣1恒成立,求实数m的取值范围.
【答案】(1)见解析;(2)(﹣∞,﹣ln2]
【解析】
(1)![]() .对
.对![]() 分类讨论,利用导数研究函数的单调性极值与最值,即可得出;(2)原命题等价于
分类讨论,利用导数研究函数的单调性极值与最值,即可得出;(2)原命题等价于![]() ,且对
,且对![]() ,
,![]() ,
,![]() 恒成立.由(1)可知:当
恒成立.由(1)可知:当![]() 时,函数
时,函数![]() 在
在![]() 单调递增,故
单调递增,故![]() 在
在![]() ,
,![]() 上单调递增,可得
上单调递增,可得![]() (1)
(1)![]() .对
.对![]() ,
,![]() ,
,![]() 恒成立
恒成立![]() 对
对![]() ,
,![]() ,
,![]() 恒成立.对
恒成立.对![]() 分类讨论:利用导数研究函数的单调性极值与最值,即可得出.
分类讨论:利用导数研究函数的单调性极值与最值,即可得出.
(1)![]() =a+
=a+![]() (x∈(0,+∞)).
(x∈(0,+∞)).
当a≥0时,![]() ≥0,
≥0,
∴f(x)在x∈(0,+∞)单调递增,无最值.
当a<0时,![]()
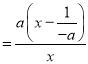 (x∈(0,+∞)).
(x∈(0,+∞)).
可得函数f(x)在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,+∞)上单调递减.
,+∞)上单调递减.
当x=![]() 时,函数f(x)取得极小值即最小值,且最大值为f(
时,函数f(x)取得极小值即最小值,且最大值为f(![]() )=﹣1﹣ln(﹣a),无最大值.
)=﹣1﹣ln(﹣a),无最大值.
(2)a>0,且对x1,x2∈[0,2],f(x1+1)≥g(x2)+a﹣1恒成立,等价于a>0,且对x∈[0,2],f(x+1)min≥g(x)max+a﹣1恒成立.
由(1)可知:当a>0时,函数f(x)在x∈(0,+∞)单调递增,故y=f(x+1)在x∈[0,2]上单调递增,
∵x∈[0,2],∴(x+1)∈[1,3],故f(x+1)min=f(1)=a.
∴对x∈[0,2],f(x+1)min≥g(x)max+a﹣1恒成立对x∈[0,2],g(x)max≤1恒成立.
对m分类讨论:m=0时,g(x)=x2,x=0,函数g(x)取得最大值,g(2)=4,不满足g(x)max≤1.
当m≠0时,![]() =2xemx+mx2emx=xemx(mx+2).令
=2xemx+mx2emx=xemx(mx+2).令![]() =0,解得x=0,x=﹣
=0,解得x=0,x=﹣![]() .
.
①当﹣![]() ≥2,即﹣1≤m<0时,对x∈[0,2],
≥2,即﹣1≤m<0时,对x∈[0,2],![]() ≥0,因此g(x)在此区间上单调递增.∴g(x)max=g(2)=4e2m.
≥0,因此g(x)在此区间上单调递增.∴g(x)max=g(2)=4e2m.
由4e2m≤1,解得m≤﹣ln2.∴﹣1≤m≤﹣ln2.
②当2>﹣![]() >0,即m<﹣1时,可得函数g(x)在x∈[0,﹣
>0,即m<﹣1时,可得函数g(x)在x∈[0,﹣![]() )上单调递增,在(﹣
)上单调递增,在(﹣![]() ,2]上单调递减.
,2]上单调递减.
∴g(x)max=g(﹣![]() )=
)=![]() e﹣2.由
e﹣2.由![]() e﹣2≤1,解得m≤﹣
e﹣2≤1,解得m≤﹣![]() .∴m<﹣1.
.∴m<﹣1.
③当﹣![]() ≤0,即m>0时,对x∈[0,2],
≤0,即m>0时,对x∈[0,2],![]() ≥0,因此g(x)在此区间上单调递增.∴g(x)max=g(2)=4e2m.
≥0,因此g(x)在此区间上单调递增.∴g(x)max=g(2)=4e2m.
此时4e2m≤1,不成立,舍去.
综上可得:实数m的取值范围是(﹣∞,﹣ln2].


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
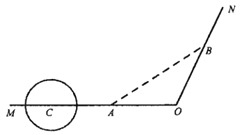
【题目】为解决城市的拥堵问题,某城市准备对现有的一条穿城公路MON进行分流,已知穿城公路MON自西向东到达城市中心![]() 后转向
后转向![]() 方向,已知∠MON=
方向,已知∠MON=![]() ,现准备修建一条城市高架道路L,L在MO上设一出入口A,在ON上设一出口B,假设高架道路L在AB部分为直线段,且要求市中心
,现准备修建一条城市高架道路L,L在MO上设一出入口A,在ON上设一出口B,假设高架道路L在AB部分为直线段,且要求市中心![]() 与AB的距离为10km.
与AB的距离为10km.
(1)求两站点A,B之间的距离;
(2)公路MO段上距离市中心![]() 30km处有一古建筑群C,为保护古建筑群,设立一个以C为圆心,5km为半径的圆形保护区.因考虑未来道路AB的扩建,则如何在古建筑群和市中心
30km处有一古建筑群C,为保护古建筑群,设立一个以C为圆心,5km为半径的圆形保护区.因考虑未来道路AB的扩建,则如何在古建筑群和市中心![]() 之间设计出入口A,才能使高架道路及其延伸段不经过保护区?
之间设计出入口A,才能使高架道路及其延伸段不经过保护区?
查看答案和解析>>
科目:高中数学 来源: 题型:
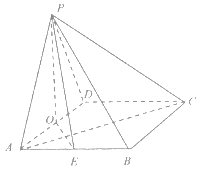
【题目】如图,四棱锥![]() 的底面是菱形,
的底面是菱形,![]() 底面
底面![]() ,
,![]() 分别是
分别是![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() .
.
(I)证明:![]() ;
;
(II)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(III)在![]() 边上是否存在点
边上是否存在点![]() ,使
,使![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() ,若存在,确定点
,若存在,确定点![]() 位置;若不存在,说明理由.
位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,A,B,C所对的边分别为a,b,c且ccosA=4,asinC=5.
(1)求边长c;
(2)著△ABC的面积S=20.求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若冬季昼夜温差x(单位:![]() )与某新品种反季节大豆的发芽数量y(单位:颗)具有线性相关关系,根据一组样本数据
)与某新品种反季节大豆的发芽数量y(单位:颗)具有线性相关关系,根据一组样本数据![]() ,用最小二乘法近似得到回归直线方程为
,用最小二乘法近似得到回归直线方程为![]() ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A.y与x具有正相关关系
B.回归直线过点![]()
C.若冬季昼夜温差增加![]() ,则该新品种反季节大豆的发芽数约增加2.5颗
,则该新品种反季节大豆的发芽数约增加2.5颗
D.若冬季昼夜温差的大小为![]() ,则该新品种反季节大豆的发芽数一定是22颗
,则该新品种反季节大豆的发芽数一定是22颗
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了适应新高考改革,某校组织了一次新高考质量测评(总分100分),在成绩统计分析中,抽取12名学生的成绩以茎叶图形式表示如图,学校规定测试成绩低于87分的为“未达标”,分数不低于87分的为“达标”.
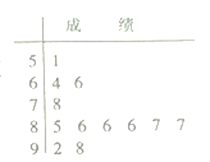
(1)求这组数据的众数和平均数;
(2)在这12名学生中从测试成绩介于80~90之间的学生中任选2人,求至少有1人“达标”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com