
【题目】已知函数f(x)=1+x﹣ ![]() +
+ ![]() ﹣
﹣ ![]() ﹣…+
﹣…+ ![]() ﹣
﹣ ![]() +
+ ![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A.f(x)在(0,1)上恰有一个零点
B.f(x)在(0,1)上恰有两个零点
C.f(x)在(﹣1,0)上恰有一个零点
D.f(x)在(﹣1,0)上恰有两个零点
【答案】C
【解析】解:函数f(x)=1+x﹣ ![]() +
+ ![]() ﹣
﹣ ![]() ﹣…+
﹣…+ ![]() ﹣
﹣ ![]() +
+ ![]() ,
,
可得f′(x)=1﹣x+x2﹣x3+…+x2012﹣x2013+x2014
=(1﹣x)+x2(1﹣x)+…+x2012(1﹣x)+x2014
=(1﹣x)(1+x2+…+x2012)+x2014 ,
当x<1时,1﹣x>0,f′(x)>0,
可得f(x)在(﹣∞,1)上递增,
由f(0)=1>0,可得f(1)>0,即有f(x)在(0,1)无零点,则A,B均错;
由f(﹣1)=1﹣1﹣ ![]() ﹣
﹣ ![]() ﹣…﹣
﹣…﹣ ![]() <0,又f(x)在(﹣1,0)递增,
<0,又f(x)在(﹣1,0)递增,
由零点存在定理,可得f(x)在(﹣1,0)上恰有一个零点.
则C正确,D错误.
故选:C.


科目:高中数学 来源: 题型:
【题目】如图,⊙O是以AB为直径的圆,点C在圆上,在△ABC和△ACD中,∠ADC=90°,∠BAC=∠CAD,DC的延长线与AB的延长线交于点E.若EB=6,EC=6 ![]() ,则BC的长为 .
,则BC的长为 . 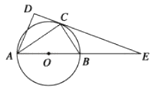
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系原点O为极点,以x轴非负半轴为极轴,以平面直角坐标系的长度单位为长度单位建立极坐标系.已知直线l的参数方程为 ![]() (t为参数),曲线C的极坐标方程为ρsin2θ=4cosθ
(t为参数),曲线C的极坐标方程为ρsin2θ=4cosθ
(Ⅰ) 求曲线C的直角坐标方程;
(Ⅱ) 设直线l与曲线C相交于A,B两点,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知焦点在x轴的椭圆的离心率与双曲线3x2-y2=3的离心率互为倒数,且过点![]() ,求:(1)求椭圆方程;
,求:(1)求椭圆方程;
(2)若直线l:y=kx+m(k≠0)与椭圆交于不同的两点M,N,点![]() ,有|MP|=|NP|,求k的取值范围.
,有|MP|=|NP|,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,OA,OB是两条互相垂直的笔直公路,半径OA=2km的扇形AOB是某地的一名胜古迹区域.当地政府为了缓解该古迹周围的交通压力,欲在圆弧AB上新增一个入口P(点P不与A,B重合),并新建两条都与圆弧AB相切的笔直公路MB,MN,切点分别是B,P.当新建的两条公路总长最小时,投资费用最低.设∠POA=![]() ,公路MB,MN的总长为
,公路MB,MN的总长为![]() .
.

(1)求![]() 关于
关于![]() 的函数关系式,并写出函数的定义域;
的函数关系式,并写出函数的定义域;
(2)当![]() 为何值时,投资费用最低?并求出
为何值时,投资费用最低?并求出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(e=2.71828…),g(x)为其反函数.
(1)求函数F(x)=g(x)﹣ax的单调区间;
(2)设直线l与f(x),g(x)均相切,切点分别为(x1 , f(x1)),(x2 , f(x2)),且x1>x2>0,求证:x1>1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com