
【题目】已知圆![]() 的圆心在
的圆心在![]() 轴上,且经过点
轴上,且经过点![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() 或
或![]()
【解析】
(1)根据题意,设![]() 的中点为
的中点为![]() ,求出
,求出![]() 的坐标,求出直线
的坐标,求出直线![]() 的斜率,由直线的点斜式方程分析可得答案,设圆
的斜率,由直线的点斜式方程分析可得答案,设圆![]() 的标准方程为
的标准方程为![]() ,由圆心的位置分析可得
,由圆心的位置分析可得![]() 的值,进而计算可得
的值,进而计算可得![]() 的值,据此分析可得答案;
的值,据此分析可得答案;
(2)设![]() 为
为![]() 的中点,结合直线与圆的位置关系,分直线
的中点,结合直线与圆的位置关系,分直线![]() 的斜率是否存在两种情况讨论,综合即可得答案.
的斜率是否存在两种情况讨论,综合即可得答案.
解:(1)设![]() 的中点为
的中点为![]() ,则
,则![]() ,
,
由圆的性质得![]() ,
,
所以![]() ,得
,得![]() ,
,
所以线段![]() 的垂直平分线方程是
的垂直平分线方程是![]() ,
,
设圆![]() 的标准方程为
的标准方程为![]() ,其中
,其中![]() ,半径为
,半径为![]() ,
,
由圆的性质,圆心![]() 在直线
在直线![]() 上,化简得
上,化简得![]() ,
,
所以圆心![]() ,
,![]() ,
,
所以圆![]() 的标准方程为
的标准方程为![]() ;
;
(2)由(1)设![]() 为
为![]() 中点,则
中点,则![]() ,得
,得![]() ,
,
圆心![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
当直线![]() 的斜率不存在时,
的斜率不存在时,![]() 的方程
的方程![]() ,此时
,此时![]() ,符合题意;
,符合题意;
当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 的方程
的方程![]() ,即
,即![]() ,
,
由题意得![]() ,解得
,解得![]() ;
;
故直线![]() 的方程为
的方程为![]() ,
,
即![]() ;
;
综上直线![]() 的方程为
的方程为![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其图象相邻两条对称轴之间的距离为
,其图象相邻两条对称轴之间的距离为![]() ,将该函数的图象向左平移
,将该函数的图象向左平移![]() 个单位后,得到的图象对应的函数为偶函数.下列判断正确的是( )
个单位后,得到的图象对应的函数为偶函数.下列判断正确的是( )
A. 函数![]() 的最小正周期为
的最小正周期为![]()
B. 函数![]() 的图象关于点
的图象关于点![]() 对称
对称
C. 函数![]() 的图象关于直线
的图象关于直线![]() 对称
对称
D. 函数![]() 在
在![]() 上单调递增
上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是公比为 q的等比数列,且a1,a3,a2成等差数列.
(Ⅰ)求q的值;
(Ⅱ)设{bn}是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业![]() 年的纯利润为
年的纯利润为![]() 万元,因设备老化等原因,企业的生产能力将逐年下降,若不进行技术改造,预测从今年(
万元,因设备老化等原因,企业的生产能力将逐年下降,若不进行技术改造,预测从今年(![]() 年)起每年比上一年纯利润减少
年)起每年比上一年纯利润减少![]() 万元,今年初该企业一次性投入资金
万元,今年初该企业一次性投入资金![]() 万元进行技术改造,预计在未扣除技术改造资金的情况下,第
万元进行技术改造,预计在未扣除技术改造资金的情况下,第![]() 年(今年为第一年)的利润为
年(今年为第一年)的利润为![]() 万元(
万元(![]() 为正整数).
为正整数).
(1)设从今年起的前![]() 年,若该企业不进行技术改造的累计纯利润为
年,若该企业不进行技术改造的累计纯利润为![]() 万元,进行技术改造后的累计纯利润为
万元,进行技术改造后的累计纯利润为![]() 万元(须扣除技术改造资金),求
万元(须扣除技术改造资金),求![]() ,
,![]() 的表达式;
的表达式;
(2)以上述预测,从今年起该企业至少经过多少年后,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(﹣1,0),B(1,0),C(0,1),直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,则b的取值范围是( )
A.(0,1)B. C.
C. D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( ).
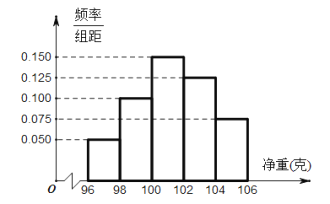
A. 90B. 75C. 60D. 45
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】棱长为1的正方体![]() 中,点
中,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上运动(不包括线段端点),且
上运动(不包括线段端点),且![]() .以下结论:①
.以下结论:①![]() ;②若点
;②若点![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 的中点,则由线
的中点,则由线![]() 与
与![]() 确定的平面在正方体
确定的平面在正方体![]() 上的截面为等边三角形;③四面体
上的截面为等边三角形;③四面体![]() 的体积的最大值为
的体积的最大值为![]() ;④直线
;④直线![]() 与直线
与直线![]() 的夹角为定值.其中正确的结论为______.(填序号)
的夹角为定值.其中正确的结论为______.(填序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com