
【题目】已知函数![]() ,
, ![]() 为常数.
为常数.
(![]() )若
)若![]() ,求
,求![]() 的取值范围.
的取值范围.
(![]() )若对任意的
)若对任意的![]() 都有不等式
都有不等式![]() 成立,求
成立,求![]() 的值.
的值.
(![]() )在(
)在(![]() )的条件下,若函数
)的条件下,若函数![]() 的图像与
的图像与![]() 轴恰有三个相异的公共点,求实数
轴恰有三个相异的公共点,求实数![]() 的取值范围.
的取值范围.
【答案】(![]() )
)![]() ;(
;(![]() )
)![]() ;(
;(![]() )
)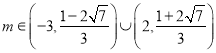 .
.
【解析】试题分析:(1)对二次项系数进行讨论,分为![]() 符合题意,
符合题意, ![]() 时,根据为此函数的性质可得不合题意,
时,根据为此函数的性质可得不合题意, ![]() 时,解一元二次不等式可得结果;(2)根据一元二次不等式的性质可得
时,解一元二次不等式可得结果;(2)根据一元二次不等式的性质可得![]() 时,不合题意,故应
时,不合题意,故应![]() ,
, ![]() ,从而可解出
,从而可解出![]() ;(3)结合(2)中的结果将其利用分段函数进行表达
;(3)结合(2)中的结果将其利用分段函数进行表达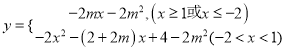 ,根据一次函数的性质可得
,根据一次函数的性质可得![]() 必有一根,解出方程得
必有一根,解出方程得![]() ,根据二次函数的性质可得
,根据二次函数的性质可得![]() 必有两个不等根,利用数形结合思想得
必有两个不等根,利用数形结合思想得![]() ,综合可得最后结果.
,综合可得最后结果.
试题解析:(![]() )当
)当![]() 时,
时, ![]() 时,
时, ![]() ,符合;
,符合;
当![]() 时,开口向下,在
时,开口向下,在![]() 上不能恒正,舍;
上不能恒正,舍;
当![]() 时,
时, ![]() ,
,
解得: ![]() 或
或![]() ,符合;综上:
,符合;综上: ![]() 的范围是
的范围是![]() .
.
(![]() )
)![]() ,
, ![]() ,对
,对![]() 恒成立,
恒成立,
当![]() 时,
时, ![]() ,不合题意(舍);当
,不合题意(舍);当![]() 时,不合题意(舍);当
时,不合题意(舍);当![]() 时,
时, ![]() ,即
,即![]() ,∴综上:
,∴综上: ![]() .
.
(![]() )
)![]() ,
,
∴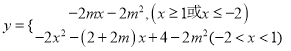 ,
,
则![]() ,必有一根,
,必有一根, ![]() ,
, ![]() 或
或![]() ,
,
![]() ,必有两个不等根,
,必有两个不等根,
∴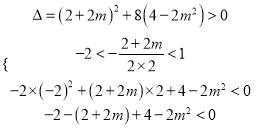 ,得
,得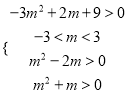 ,
,
综上: ![]() 范围
范围 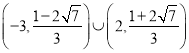 .
.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
. ![]() 在
在![]() 上有最大值9,最小值4.
上有最大值9,最小值4.
(1)求实数![]() 的值;
的值;
(2)若不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若方程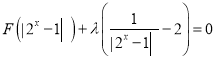 有三个不同的实数根,求实数
有三个不同的实数根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“a=﹣1”是“直线ax+3y+2=0与直线x+(a﹣2)y+1=0平行”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
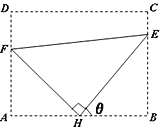
【题目】如图,某污水处理厂要在一个矩形污水处理池![]() 的池底水平铺设污水净化管道(
的池底水平铺设污水净化管道(![]() ,
, ![]() 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口
是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口![]() 是
是![]() 的中点,
的中点, ![]() 分别落在线段
分别落在线段![]() 上.已知
上.已知![]() 米,
米, ![]() 米,记
米,记![]() .
.
(1)试将污水净化管道的总长度![]() (即
(即![]() 的周长)表示为
的周长)表示为![]() 的函数,并求出定义域;
的函数,并求出定义域;
(2)问![]() 当取何值时,污水净化效果最好?并求出此时管道的总长度.
当取何值时,污水净化效果最好?并求出此时管道的总长度.
(提示: ![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设正三棱锥A﹣BCD(底面是正三角形,顶点在底面的射影为底面中心)的所有顶点都在球O的球面上,BC=2,E,F分别是AB,BC的中点,EF⊥DE,则球O的表面积为( )
A.![]()
B.6π
C.8π
D.12π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() .(14分)
.(14分)
(1)此方程表示圆,求m的取值范围;
(2)若(1)中的圆与直线x+2y-4=0相交于M、N两点,且![]() (O为坐标原点),求m的值;
(O为坐标原点),求m的值;
(3)在(2)的条件下,求以![]() 为直径的圆的方程.
为直径的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的个数是( )
①函数f(x)=2x﹣x2的零点有2个;
②函数y=sin(2x+ ![]() )sin(
)sin( ![]() ﹣2x)的最小正周期是π;
﹣2x)的最小正周期是π;
③命题“函数f(x)在x=x0处有极值,则f′(x0)=0”的否命题是真命题;
④ ![]() dx=
dx= ![]() .
.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,设二次函数
中,设二次函数![]() 的图像与两坐标轴有三个交点,经过这三点的圆记为
的图像与两坐标轴有三个交点,经过这三点的圆记为![]()
(1)求圆![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与圆
与圆![]() 相交,所截得的弦长为4,求直线
相交,所截得的弦长为4,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com