
已知函数 (
( ).
).
(I)若 的定义域和值域均是
的定义域和值域均是 ,求实数
,求实数 的值;
的值;
(II)若 在区间
在区间 上是减函数,且对任意的
上是减函数,且对任意的 ,
,
 ,总有
,总有 ,求实数
,求实数 的取值范围.
的取值范围.
(I) a=2, (II)  .
.
解析试题分析:(I)研究二次函数性质,关键研究对称轴与定义区间之间相对位置关系. 因为函数f(x)对称轴为x=a,抛物线开口向上,在 (1,a)上单调递减,则f(1)=a,f(a)=1,代入 解得a=2, (II) 因为
解得a=2, (II) 因为 在区间
在区间 上是减函数,所以
上是减函数,所以 因此
因此 ,所以1离开对称轴的距离最远,所以在区间
,所以1离开对称轴的距离最远,所以在区间 最大值应为
最大值应为 ,最小值应为
,最小值应为 ,因此对任意的
,因此对任意的 ,
,
 ,总有
,总有 ,就可化为
,就可化为 ,
, ,解得
,解得 ,又
,又 所以
所以
(1)因为函数f(x)对称轴为x=a,抛物线开口向上,在 (1,a)上单调递减,
则f(1)=a,f(a)=1,代入解得a=2 -6分
(2)可得 ,显然在区间
,显然在区间 最大值应为
最大值应为 ,最小值应为
,最小值应为
所以 ,解得
,解得 -14分
-14分
考点:二次函数最值


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)的定义域为{x|x∈R,且x≠0},对定义域内的任意x1、x2,都有f(x1·x2)=f(x1)+f(x2),且当x>1时,f(x)>0.
(1)求证:f(x)是偶函数;
(2)求证:f(x)在(0,+∞)上是增函数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
据环保部门测定,某处的污染指数与附近污染源的强度成正比,与到污染源距离的平方成反比,比例常数为
 .现已知相距18
.现已知相距18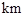 的A,B两家化工厂(污染源)的污染强度分别为
的A,B两家化工厂(污染源)的污染强度分别为 ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数 等于两化工厂对该处的污染指数之和.设
等于两化工厂对该处的污染指数之和.设 (
(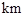 ).
).
(1)试将 表示为
表示为 的函数; (2)若
的函数; (2)若 ,且
,且 时,
时, 取得最小值,试求
取得最小值,试求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知 (
( )
)
(1)若方程 有3个不同的根,求实数
有3个不同的根,求实数 的取值范围;
的取值范围;
(2)在(1)的条件下,是否存在实数 ,使得
,使得 在
在 上恰有两个极值点
上恰有两个极值点 ,且满足
,且满足 ,若存在,求实数
,若存在,求实数 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知

(1)当 时,求
时,求 的极大值点;
的极大值点;
(2)设函数 的图象
的图象 与函数
与函数 的图象
的图象 交于
交于 、
、 两点,过线段
两点,过线段 的中点做
的中点做 轴的垂线分别交
轴的垂线分别交 、
、 于点
于点 、
、 ,证明:
,证明: 在点
在点 处的切线与
处的切线与 在点
在点 处的切线不平行.
处的切线不平行.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com