
【题目】已知函数![]() .
.
(Ⅰ)记![]() ,当
,当![]() 时,恒有
时,恒有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() ,求证:对任意
,求证:对任意![]() ,
,![]() 与
与![]() 在
在![]() 上有唯一公共点.
上有唯一公共点.
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为D,若存在实常数
的定义域为D,若存在实常数![]() 及
及![]() ,对任意
,对任意![]() ,当
,当![]() 且
且![]() 时,都有
时,都有![]() 成立,则称函数
成立,则称函数![]() 具有性质
具有性质![]() .
.
(1)判断函数![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(2)若函数![]() 具有性质
具有性质![]() ,求
,求![]() 及
及![]() 应满足的条件;
应满足的条件;
(3)已知函数![]() 不存在零点,当
不存在零点,当![]() 时具有性质
时具有性质![]() (其中
(其中![]() ,
,![]() ),记
),记![]() ,求证:数列
,求证:数列![]() 为等比数列的充要条件是
为等比数列的充要条件是![]() 或
或![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+lnx(a∈R).
(1)当a=![]() 时,求f(x)在区间[1,e]上的最大值和最小值;
时,求f(x)在区间[1,e]上的最大值和最小值;
(2)如果函数g(x),f1(x),f2(x),在公共定义域D上,满足f1(x)<g(x)<f2(x),那么就称g(x)为f1(x),f2(x)的“活动函数”.已知函数![]() .
. ![]() 。若在区间(1,+∞)上,函数f(x)是f1(x),f2(x)的“活动函数”,求a的取值范围.
。若在区间(1,+∞)上,函数f(x)是f1(x),f2(x)的“活动函数”,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在衡阳市“创全国文明城市”(简称“创文”)活动中,市教育局对本市A,B,C,D四所高中学校按各校人数分层抽样,随机抽查了200人,将调查情况进行整理后制成下表:
学校 | A | B | C | D |
抽查人数 | 10 | 15 | 100 | 75 |
“创文”活动中参与的人数 | 9 | 10 | 80 | 49 |
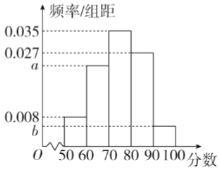
假设每名高中学生是否参与“创文”活动是相互独立的
(1)若本市共8000名高中学生,估计C学校参与“创文”活动的人数;
(2)在上表中从A,B两校没有参与“创文”活动的同学中随机抽取2人,求恰好A,B两校各有1人没有参与“创文”活动的概率;
(3)在随机抽查的200名高中学生中,进行文明素养综合素质测评(满分为100分),得到如上的频率分布直方图,其中![]() .求a,b的值,并估计参与测评的学生得分的中位数.(计算结果保留两位小数).
.求a,b的值,并估计参与测评的学生得分的中位数.(计算结果保留两位小数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是正方形,点
是正方形,点![]() 在以
在以![]() 为直径的半圆弧上(
为直径的半圆弧上(![]() 不与
不与![]() ,
,![]() 重合),
重合),![]() 为线段
为线段![]() 的中点,现将正方形
的中点,现将正方形![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
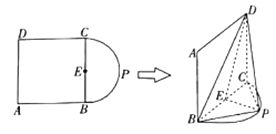
(1)证明:![]() 平面
平面![]() .
.
(2)若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,求
的体积最大时,求![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,E是棱AB的中点,动点F是侧面ACC1A1(包括边界)上一点,若EF//平面BCC1B1,则动点F的轨迹是( )
A.线段B.圆弧
C.椭圆的一部分D.抛物线的一部分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com