
【题目】已知函数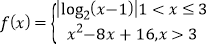 若方程f(x)=m有4个不同的实根x1,x2,x3,x4,且x1<x2<x3<x4,则(
若方程f(x)=m有4个不同的实根x1,x2,x3,x4,且x1<x2<x3<x4,则(![]() )(x3+x4)=( )
)(x3+x4)=( )
A. 6 B. 7 C. 8 D. 9
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的最小值为-1,且关于
的最小值为-1,且关于![]() 的方程
的方程![]() 的两根为0和-2.
的两根为0和-2.
(1)求函数![]() 的解析式;
的解析式;
(2)设![]() 其中
其中![]() ,求函数
,求函数![]() 在
在![]() 时的最大值
时的最大值![]() ;
;
(3)若![]() (
(![]() 为实数),对任意
为实数),对任意![]() ,总存在
,总存在![]() 使得
使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知动点![]() 都在曲线
都在曲线![]() (
(![]() 为参数,
为参数,![]() 是与
是与![]() 无关的正常数)上,对应参数分别为
无关的正常数)上,对应参数分别为![]() 与
与![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)求![]() 的轨迹的参数方程;
的轨迹的参数方程;
(2)作一个伸压变换:![]() ,求出动点
,求出动点![]() 点的参数方程,并判断动点
点的参数方程,并判断动点![]() 的轨迹能否过点
的轨迹能否过点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(多选)下列命题中为真命题的是( )
A.若事件![]() 与事件
与事件![]() 互为对立事件,则事件
互为对立事件,则事件![]() 与事件
与事件![]() 为互斥事件
为互斥事件
B.若事件![]() 与事件
与事件![]() 为互斥事件,则事件
为互斥事件,则事件![]() 与事件
与事件![]() 互为对立事件
互为对立事件
C.若事件![]() 与事件
与事件![]() 互为对立事件,则事件
互为对立事件,则事件![]() 为必然事件
为必然事件
D.若事件![]() 为必然事件,则事件
为必然事件,则事件![]() 与事件
与事件![]() 为互斥事件
为互斥事件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北![]() 的方向上,仰角为
的方向上,仰角为![]() ,行驶4km后到达B处,测得此山顶在西偏北
,行驶4km后到达B处,测得此山顶在西偏北![]() 的方向上.
的方向上.
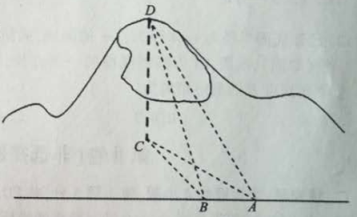
(1)求此山的高度(单位:km);
(2)设汽车行驶过程中仰望山顶D的最大仰角为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面是水稻产量与施化肥量的一组观测数据(单位:千克/亩):
施化肥量 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
水稻产量 | 320 | 330 | 360 | 410 | 460 | 470 | 480 |
(1)将上述数据制成散点图;
(2)你能从散点图中发现施化肥量与水稻产量近似成什么关系吗?水稻产量会一直随施化肥量的增加而增长吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级的一次月考成绩中随机抽取了 50名学生的成绩(满分100分,且抽取的学生成绩都在![]() 内),按成绩分为
内),按成绩分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五组,得到如图所示的频率分布直方图.
五组,得到如图所示的频率分布直方图.
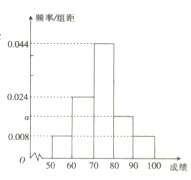
(1)用分层抽样的方法从月考成绩在![]() 内的学生中抽取6人,求分别抽取月考成绩在
内的学生中抽取6人,求分别抽取月考成绩在![]() 和
和![]() 内的学生多少人;
内的学生多少人;
(2)在(1)的前提下,从这6名学生中随机抽取2名学生进行调查,求月考成绩在![]() 内至少有1名学生被抽到的概率.
内至少有1名学生被抽到的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com