
分析 (1)利用同角三角函数基本关系式化简所求即可得解;
(2)利用同角三角函数基本关系式化简所求即可得解;
解答 解:已知tanα=$\frac{1}{2}$,
(1)$\frac{sinα+2cosα}{2sinα-3cosα}$=$\frac{tanα+2}{2tanα-3}$=$\frac{\frac{1}{2}+2}{2×\frac{1}{2}-3}$=-$\frac{5}{4}$;
(2)sin2α+2sinαcosα=$\frac{si{n}^{2}α+2sinαcosα}{si{n}^{2}α+co{s}^{2}α}$=$\frac{ta{n}^{2}α+2tanα}{ta{n}^{2}α+1}$=$\frac{\frac{1}{4}+2×\frac{1}{2}}{\frac{1}{4}+1}$=1.
点评 本题主要考查了同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
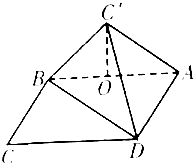 如图.在矩形ABCD中.AB=3 $\sqrt{3}$,BC=3,沿对角线BD把△BCD折起.使C移到C′.且C′在面ABC内的射影O恰好落在AB上.
如图.在矩形ABCD中.AB=3 $\sqrt{3}$,BC=3,沿对角线BD把△BCD折起.使C移到C′.且C′在面ABC内的射影O恰好落在AB上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com