
����Ŀ��ijְ�ƽ������������Բμ�ij��רҵ�������Ե�100�˵ijɼ�������ͳ�ƣ�������Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ�����涨80�ּ������߽����ɹ����������ʧ�ܣ�

�����ɹ� | ����ʧ�� | �ϼ� | |
�� | 16 | ||
Ů | 50 | ||
�ϼ� |
��1����ͼ��![]() ��ֵ��
��ֵ��
��2��������֪�����������![]() �����������ж��ܷ���
�����������ж��ܷ���![]() �İ�����Ϊ�������ɹ������Ա��йأ�
�İ�����Ϊ�������ɹ������Ա��йأ�
��3����Ƶ����Ϊ���ʣ��ӱ��ο��Ե�������Ա�У������ȡ4�˽���Լ̸������4���н���ʧ�ܵ�����Ϊ![]() ����
����![]() �ķֲ�������ѧ����
�ķֲ�������ѧ����![]() ��
��
���ο���ʽ��![]() ������
������![]() ��
��
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
���𰸡�(1) ![]() ��(2)���������������г���
��(2)���������������г���![]() �İ�����Ϊ�������ɹ������Ա��йأ�(3)�ֲ��м�������
�İ�����Ϊ�������ɹ������Ա��йأ�(3)�ֲ��м�������![]() =3
=3
��������
��1����Ƶ�ʺ�Ϊ1���г�������![]() ��ֵ��
��ֵ��
��2����Ƶ�ʷֲ�ֱ��ͼ��������ɹ���Ƶ�ʣ���������ɹ���������
��д![]() ������������۲�ֵ�������ٽ�ֵ�ó����ۣ�
������������۲�ֵ�������ٽ�ֵ�ó����ۣ�
��3����Ƶ�ʷֲ�ֱ��ͼ֪����ʧ�ܵ�Ƶ�ʣ���Ƶ����Ϊ���ʣ�
֪�������![]() ���Ӷ���ֲ��������Ӧ�ĸ���ֵ��д���ֲ��У�������ѧ����.
���Ӷ���ֲ��������Ӧ�ĸ���ֵ��д���ֲ��У�������ѧ����.
�⣺��1����Ƶ�ʷֲ�ֱ��ͼ��С����������ܺ�Ϊ1��
��֪![]() ��
��
���![]() ��
��
��2����Ƶ�ʷֲ�ֱ��ͼ֪�������ɹ���Ƶ��Ϊ![]() ��
��
���Խ����ɹ�������Ϊ![]() ���ˣ���
���ˣ���
������£�
�����ɹ� | ����ʧ�� | �ϼ� | |
�� | 16 | 34 | 50 |
Ů | 9 | 41 | 50 |
�ϼ� | 25 | 75 | 100 |
���衰�����ɹ������Ա��أ�
�����ϱ����ݴ��빫ʽ�ɵ�![]() ��
��
�����г���![]() �İ�����Ϊ�������ɹ������Ա��йأ�
�İ�����Ϊ�������ɹ������Ա��йأ�
��3����Ƶ�ʷֲ�ֱ��ͼ֪����ʧ�ܵ�Ƶ��Ϊ![]() ��
��
��Ƶ����Ϊ���ʣ�
��ӱ��ο��Ե�������Ա�У������ȡ1�˽���Լ̸�����˽���ʧ�ܵĸ���Ϊ0.75��
����![]() ����Ϊ���Ӷ���ֲ�����
����Ϊ���Ӷ���ֲ�����![]() ��
��
![]()
![]() ��
��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() .
.
����![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
��ѧ����Ϊ![]() .��
.��![]() ����
����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ������![]() ��ͼ����һ�����ĶԳ�ͼ�Σ����ڵ�
��ͼ����һ�����ĶԳ�ͼ�Σ����ڵ�![]() �Գƣ���ô��
�Գƣ���ô��![]() ��ͼ������ƽ��m����λ������ƽ��n�ĵ�λ��õ�һ������ԭ��ԳƵĺ���ͼ��.������
��ͼ������ƽ��m����λ������ƽ��n�ĵ�λ��õ�һ������ԭ��ԳƵĺ���ͼ��.������![]() Ϊ�溯��.��ô����������������ĸ����ǣ� ��
Ϊ�溯��.��ô����������������ĸ����ǣ� ��
�ٶ��κ���![]() ��
��![]() ����ͼ��϶�����һ�����ĶԳ�ͼ�Σ�
����ͼ��϶�����һ�����ĶԳ�ͼ�Σ�
�������![]() ��
��![]() ����ͼ��϶���һ�����ĶԳ�ͼ�Σ�
����ͼ��϶���һ�����ĶԳ�ͼ�Σ�
�ۺ���![]() ��
��![]() ��
��![]() ����ͼ��϶���һ�����ĶԳ�ͼ��.
����ͼ��϶���һ�����ĶԳ�ͼ��.
A.0��B.1��C.2��D.3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������D�ϵĺ���f��x�����㣺������x��D�����ڳ���M>0������-M<f��x��<M���������f��x����D�ϵ��н纯��������M��Ϊ����f��x�����Ͻ硣
�����жϺ���f��x��=![]() -2x+2��x��[0��2]�Ƿ����н纯������˵�����ɣ�
-2x+2��x��[0��2]�Ƿ����н纯������˵�����ɣ�
����������f��x��=1+![]() +
+![]() ��x��[0��+�ޣ�����3Ϊ�Ͻ���н纯������ʵ��a��ȡֵ��Χ��
��x��[0��+�ޣ�����3Ϊ�Ͻ���н纯������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ��ռ�ֱ������ϵO��xyz�У�����P��x0��y0��z0����һ��������Ϊ![]() ����a��b��c����ƽ�����ķ���Ϊa��x��x0��+b��y��y0��+c��z��z0����0������P��x0��y0��z0����һ����������Ϊ
����a��b��c����ƽ�����ķ���Ϊa��x��x0��+b��y��y0��+c��z��z0����0������P��x0��y0��z0����һ����������Ϊ![]() ����u��v��w����uvw��0����ֱ��l�ķ���Ϊ
����u��v��w����uvw��0����ֱ��l�ķ���Ϊ![]() ���Ķ�������ϣ�������������⣺��֪ƽ�����ķ���Ϊx+2y��2z��4��0��ֱ��l����ƽ��3x��2y��7��0��2y��z+6��0�Ľ��ߣ���ֱ��l��ƽ�������ɽǵĴ�СΪ��������
���Ķ�������ϣ�������������⣺��֪ƽ�����ķ���Ϊx+2y��2z��4��0��ֱ��l����ƽ��3x��2y��7��0��2y��z+6��0�Ľ��ߣ���ֱ��l��ƽ�������ɽǵĴ�СΪ��������
A. arcsin![]() B. arcsin
B. arcsin![]()
C. arcsin![]() D. arcsin
D. arcsin![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ľ��飬ij��������ʩ���ڼ�Ľ�ˮ��![]() ����λ��
����λ��![]() ���Թ��ڵ�Ӱ�����±���
���Թ��ڵ�Ӱ�����±���

����ij����վ�����ϣ�ij����С�鳭¼�˸ù���ʩ����ij��ǰ20��Ľ�ˮ�������ݣ����Ƶõ���ˮ��������ͼ������ͼ��ʾ.
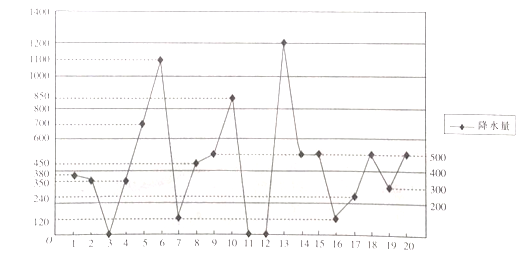
��1������20���ƽ����ˮ����
��2�����ݽ�ˮ��������ͼ���ֱ���Ƹù���ʩ����������![]() �ĸ���.
�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-5������ʽѡ��
��֪����![]() .
.
��1����ʽ![]() �Ľ⼯��
�Ľ⼯��
��2����![]() ��
��![]() ���������
���������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ԭ�㣬������x���ϵ���ԲC��������Ϊ![]() ���Ҿ�����M(1��
���Ҿ�����M(1��![]() ��������P(2,1����ֱ��l����ԲC�ཻ�ڲ�ͬ������A��B.
��������P(2,1����ֱ��l����ԲC�ཻ�ڲ�ͬ������A��B.
��1������ԲC�ķ��̣�
��2���Ƿ����ֱ��l������![]() �������ڣ����ֱ��l�ķ��̣��������ڣ���˵�����ɣ�
�������ڣ����ֱ��l�ķ��̣��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)����![]() �ķ���
�ķ���![]() ǡ����������ȵ�ʵ����,��ʵ��
ǡ����������ȵ�ʵ����,��ʵ��![]() ��ֵ.
��ֵ.
(2)����![]() �ķ���
�ķ���![]() ��
��![]() ��ǡ����������ʵ����,��ʵ��
��ǡ����������ʵ����,��ʵ��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com