
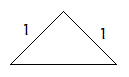
【题目】已知一个四棱锥的正视图和侧视图为两个完全相同的等腰直角三角形(如图示),腰长为1,则该四棱锥的体积为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+ax,(a∈R),其图象与x轴交于A(x1 , 0),B(x2 , 0)两点,且x1<x2
(1)求a的取值范围;
(2)证明: ![]() ;(f′(x)为f(x)的导函数)
;(f′(x)为f(x)的导函数)
(3)设点C在函数f(x)的图象上,且△ABC为等边三角形,记 ![]() ,求(t﹣1)(a+
,求(t﹣1)(a+ ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等比数列![]() 的前
的前![]() 项和为
项和为![]() ;数列
;数列![]() 满足
满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)①试确定![]() 的值,使得数列
的值,使得数列![]() 为等差数列;
为等差数列;
②在①结论下,若对每个正整数![]() ,在
,在![]() 与
与![]() 之间插入
之间插入![]() 个2,得到一个新数列
个2,得到一个新数列![]() ,设
,设![]() 是数列
是数列![]() 的前
的前![]() 项和,试求满足
项和,试求满足![]() 的所有正整数
的所有正整数![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·上海)设z1, z2![]() C, ,则“z1, z2中至少有一个数是虚数”是“z1-z2是虚数”的( )
C, ,则“z1, z2中至少有一个数是虚数”是“z1-z2是虚数”的( )
A.充分非必要条件
B.必要非充分条件
C.充要条件
D.既非充分又非必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的前n项和为Sn=a2n+b,且a1=3.
(1)求a、b的值及数列{an}的通项公式;
(2)设bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com