
分析 (1)求出函数的导数,计算f(0),f′(0),求出切线方程即可;
(2)令F(x)=f(x)-l(x),求出函数F(x)的导数,解关于导函数的不等式,求出函数的单调区间,从而求出F(x)的最小值,证出结论即可;
(3)问题转化为2sinx-2cosx-2x+2≥0恒成立,只需证-e1-2x≤2x-2在$x∈[{-\frac{1}{2},1}]$时恒成立即可设函数h(x)=2x-2+e1-2x,$x∈[-\frac{1}{2},1]$,根据函数的单调性证明即可.
解答 解:(1)由题意可知,f'(x)=2cosx+2sinx,
f'(0)=2,f(0)=-2,
所以f(x)在x=0处的切线方程y=2x-2;
(2)证明:令F(x)=f(x)-l(x)=2sinx-2cosx-2x+2,$x∈[{-\frac{1}{2},1}]$
则$F'(x)=2cosx+2sinx-2=2\sqrt{2}sin({x+\frac{π}{4}})-2$
当x∈(0,1]时,F'(x)>0,即F(x)在(0,1]上是增函数,
当$x∈[-\frac{1}{2},0)$时,F'(x)<0,即F(x)在$[-\frac{1}{2},0)$上是减函数,
所以,在$[-\frac{1}{2},1]$上,F(x)min=F(0)=0,所以F(x)≥0.
所以,f(x)≥l(x),(当且仅当x=0时上式取等号)
(3)欲证$x∈[{-\frac{1}{2},1}]$,f(x)+g(x)≥0
需证$-{e^{1-2x}}<2\sqrt{2}sin(x-\frac{π}{4})$,对于任意$x∈[-\frac{1}{2},1]$上恒成立,
由(2)知$x∈[{-\frac{1}{2},1}]$时,f(x)≥l(x)恒成立;
即2sinx-2cosx-2x+2≥0恒成立
所以,现只需证-e1-2x≤2x-2在$x∈[{-\frac{1}{2},1}]$时恒成立即可
设函数h(x)=2x-2+e1-2x,$x∈[-\frac{1}{2},1]$,
则h′(x)=2-2e1-2x=2(1-e1-2x),
当$x∈[-\frac{1}{2},\frac{1}{2})$时,h′(x)<0,即h(x)在$[-\frac{1}{2},\frac{1}{2})$上是减函数,
当$x∈(\frac{1}{2},1]$时,h′(x)>0,即h(x)在$(\frac{1}{2},1]$上是增函数,
所以在$[-\frac{1}{2},1]$上,$h{(x)_{min}}=h(\frac{1}{2})=0$,所以h(x)≥0,即-e1-2x≤2x-2,
(当且仅当$x=\frac{1}{2}$时上式取等号)②,
综上所述,$-{e^{1-2x}}≤2x-2≤2\sqrt{2}sin(x-\frac{π}{4})$,
所以$x∈[{-\frac{1}{2},1}]$时,f(x)+g(x)≥0恒成立.
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用以及不等式的证明,是一道综合题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | A∈l,A∈α,B∈α⇒l?α | |
| B. | l?α,A∈l⇒A∉α | |
| C. | A∈α,A∈β,B∈α,B∈β⇒α∩β=AB | |
| D. | A,B,C∈α,A,B,C∈β且A,B,C不共线⇒α,β重合 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 10 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
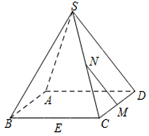 如图,在正四棱锥S-ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论:
如图,在正四棱锥S-ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论:| A. | ①③ | B. | ③④ | C. | ①② | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 45° | C. | 30° | D. | 90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com