Question

【题目】圆过点， .

求：（1）周长最小的圆的方程；

（2）圆心在直线上的圆的方程.

Answer 1

【答案】（1）x2＋(y－1)2＝10（2）(x－3)2＋(y－2)2＝20

【解析】试题分析:(1)当周长最小时为圆的直径，由此可得所求圆的圆心和半径，即可得圆的方程；（2）线段的垂直平分线与直线的交点即为圆心坐标, 即为半径，可得圆的方程.

解:(1)当AB为直径时，过A、B的圆的半径最小，从而周长最小．即AB中点(0,1)为圆心，半径r＝|AB|＝.则圆的方程为：x2＋(y－1)2＝10.

(2) 解法1：AB的斜率为k＝－3，则AB的垂直平分线的方程是y－1＝x.即x－3y＋3＝0

由圆心在直线上得两直线交点为圆心即圆心坐标是C(3,2)．

r＝|AC|＝＝2.∴圆的方程是(x－3)2＋(y－2)2＝20.

解法2：待定系数法

设圆的方程为：(x－a)2＋(y－b)2＝r2.

则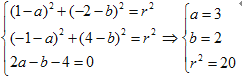

∴圆的方程为：(x－3)2＋(y－2)2＝20.