
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,若函数
时,若函数![]() 在
在![]() 上有且只有一个零点,求实数
上有且只有一个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)详见解析 (2)![]()
【解析】
(1)求得函数的导数![]() ,分
,分![]() 和
和![]() ,两种情况讨论,即可求得函数的单调区间;
,两种情况讨论,即可求得函数的单调区间;
(2)①当![]() 时,根据
时,根据![]() ,求得
,求得![]() 在
在![]() 上只有一个零点;②当
上只有一个零点;②当![]() 时,分
时,分![]() 、
、![]() 和
和![]() ,三种情况讨论,结合函数的单调性和零点的存在定理,即可求解.
,三种情况讨论,结合函数的单调性和零点的存在定理,即可求解.
(1)由题意,函数![]() 的定义域为
的定义域为![]() ,
,
且![]() ,
,
①当![]() 时,令
时,令![]() ,即
,即![]() .解得
.解得![]() ;
;
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以![]() 在
在![]() 上单调递减,
上单调递减,![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,由
时,由![]() ,得
,得![]() 或
或![]()
(i)若![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递增;
上单调递增;
(ii)若![]() ,则
,则![]() ,令
,令![]() ,可得
,可得![]() 或
或![]() ;
;
令![]() ,解得
,解得![]() ,
,
所以函数![]() 在
在![]() ,
,![]() 上单调递增,
上单调递增,![]() 在
在![]() 上单调递减;
上单调递减;
(iii)若![]() ,则
,则![]() ,令
,令![]() ,解得
,解得![]() 或
或![]() ;
;
令![]() ,解得
,解得![]() ,
,
所以函数![]() 在
在![]() 上单调递增,
上单调递增,![]() 在
在![]() 上单调递减.
上单调递减.
(2)①当![]() 时,函数
时,函数![]() ,令
,令![]() 得
得![]() ,
,
又知当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
此时![]() 在
在![]() 上有且只有一个零点;
上有且只有一个零点;
②当![]() 时,
时,
(i)当![]() 时,由(1)知
时,由(1)知![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,
此时![]() 在
在![]() 上有且只有一个零点;
上有且只有一个零点;
(ii)当![]() 时,由(1)结合
时,由(1)结合![]() 的单调性,
的单调性,![]() ,只需讨论
,只需讨论![]() 的符号,
的符号,
当![]() 时,由
时,由![]() ,可得
,可得![]() 在
在![]() 上有且只有一个零点;
上有且只有一个零点;
当时![]() 时,由
时,由![]() ,可得
,可得![]() 在
在![]() 上无零点;
上无零点;
(iii)若![]() 由(1)结合
由(1)结合![]() 的单调性,
的单调性,![]() ,
,
![]() ,此时
,此时![]() 在
在![]() 上有且只有一个零点,
上有且只有一个零点,
综上所述,实数![]() 的取值范围
的取值范围![]() .
.


科目:高中数学 来源: 题型:
【题目】双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,
,![]() 为坐标原点.
为坐标原点.![]() 为曲线
为曲线![]() 右支上的点,点
右支上的点,点![]() 在
在![]() 外角平分线上,且
外角平分线上,且![]() .若
.若![]() 恰为顶角为
恰为顶角为![]() 的等腰三角形,则该双曲线的离心率为( )
的等腰三角形,则该双曲线的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某超市2018年12个月的收入与支出数据的折线图如图所示:
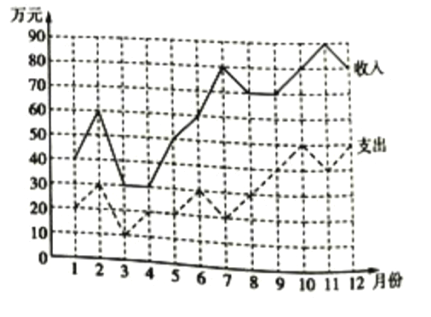
根据该折线图可知,下列说法错误的是( )
A. 该超市2018年的12个月中的7月份的收益最高
B. 该超市2018年的12个月中的4月份的收益最低
C. 该超市2018年1-6月份的总收益低于2018年7-12月份的总收益
D. 该超市2018年7-12月份的总收益比2018年1-6月份的总收益增长了90万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“干支纪年法”是中国历法自古以来就使用的纪年方法,甲、乙、丙、丁、戊、已、庚、辛、壬、癸为十天干;子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥为十二地支.“干支纪年法”是以一个天干和一个地支按上述顺序相配排列起来,天干在前,地支在后,已知2017年是丁酉年,2018年是戊戌年,2019年是已亥年,依此类推,则2080年是____________年.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点P为平面上的动点,过点P作直线l:
,点P为平面上的动点,过点P作直线l:![]() 的垂线,垂足为Q,且
的垂线,垂足为Q,且![]() .
.
![]() Ⅰ
Ⅰ![]() 求动点P的轨迹C的方程;
求动点P的轨迹C的方程;
![]() Ⅱ
Ⅱ![]() 设点P的轨迹C与x轴交于点M,点A,B是轨迹C上异于点M的不同的两点,且满足
设点P的轨迹C与x轴交于点M,点A,B是轨迹C上异于点M的不同的两点,且满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,焦点为
上,焦点为![]() ,圆O的直径为
,圆O的直径为![]() .
.

(1)求椭圆C及圆O的标准方程;
(2)设直线l与圆O相切于第一象限内的点P,且直线l与椭圆C交于![]() 两点.记
两点.记![]() 的面积为
的面积为![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有大小相同的红、黄两种颜色的球各1个,从中任取1只,有放回地抽取3次.
求:(1)3只全是红球的概率;
(2)3只颜色全相同的概率;
(3)3只颜色不全相同的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,圆![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线
轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 是
是![]() 上一动点,求点
上一动点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com