
【题目】(本小题满分14分)
已知![]() ,
, ![]() 为椭圆
为椭圆![]() 的左、右顶点,
的左、右顶点, ![]() 为其右焦点,
为其右焦点, ![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
, ![]() 的动点,且
的动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(Ⅰ)求椭圆![]() 的方程及离心率;
的方程及离心率;
(Ⅱ)直线![]() 与椭圆在点
与椭圆在点![]() 处的切线交于点
处的切线交于点![]() ,当直线
,当直线![]() 绕点
绕点![]() 转动时,试判断以
转动时,试判断以![]()
为直径的圆与直线![]() 的位置关系,并加以证明.
的位置关系,并加以证明.
【答案】解:(Ⅰ)由题意可设椭圆![]() 的方程为
的方程为![]() ,
, ![]() .
.
由题意知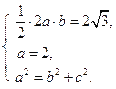 解得
解得![]() ,
, ![]() .
.
故椭圆![]() 的方程为
的方程为![]() ,离心率为
,离心率为![]() .……6分
.……6分
(Ⅱ)以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
证明如下:由题意可设直线![]() 的方程为
的方程为![]()
![]() .
.
则点![]() 坐标为
坐标为![]() ,
, ![]() 中点
中点![]() 的坐标为
的坐标为![]() .
.
由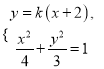 得
得![]() .
.
设点![]() 的坐标为
的坐标为![]() ,则
,则![]() .
.
所以![]() ,
, ![]() .……………………………10分
.……………………………10分
因为点![]() 坐标为
坐标为![]() ,
,
当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
直线![]() 轴,此时以
轴,此时以![]() 为直径的圆
为直径的圆![]() 与直线
与直线![]() 相切.
相切.
当![]() 时,则直线
时,则直线![]() 的斜率
的斜率![]() .
.
所以直线![]() 的方程为
的方程为![]() .
.
点![]() 到直线
到直线![]() 的距离
的距离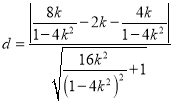
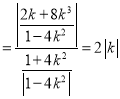 .
.
又因为![]() ,所以
,所以![]() .
.
故以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
综上得,当直线![]() 绕点
绕点![]() 转动时,以
转动时,以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.………14分
相切.………14分
【解析】试题分析:(Ⅰ)根据椭圆的特征可得当点![]() 在点
在点![]() 时,
时, ![]() 面积最大,即可列
面积最大,即可列![]() ,由题目条件知
,由题目条件知![]() ,结合
,结合![]() ,进而求得椭圆
,进而求得椭圆![]() 的方程及离心率;
的方程及离心率;
(Ⅱ)设![]() ,由题意可设直线
,由题意可设直线![]() 的方程为
的方程为![]() ,可得点
,可得点![]() 与
与![]() 中点
中点![]() 的坐标,联立直线与椭圆的方程得
的坐标,联立直线与椭圆的方程得![]() ,进而表示出点
,进而表示出点![]() 的坐标,结合点
的坐标,结合点![]() ,再写出直线
,再写出直线![]() 的方程,根据点
的方程,根据点![]() 到直线
到直线![]() 的距离等于直径
的距离等于直径![]() 的一半,进而解得此问.
的一半,进而解得此问.
试题解析:(Ⅰ)由题意可设椭圆![]() 的方程为
的方程为![]() ,
, ![]() .
.
由题意知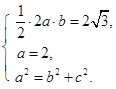 解得
解得![]() ,
, ![]() .
.
故椭圆![]() 的方程为
的方程为![]() ,离心率为
,离心率为![]() .
.
(Ⅱ)以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
证明如下:由题意可设直线![]() 的方程为
的方程为![]()
![]() .
.
则点![]() 坐标为
坐标为![]() ,
, ![]() 中点
中点![]() 的坐标为
的坐标为![]() .
.
由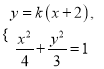 得
得![]() .
.
设点![]() 的坐标为
的坐标为![]() ,则
,则![]() .
.
所以![]() ,
, ![]() .
.
因为点![]() 坐标为
坐标为![]() ,
,
当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
直线![]() 轴,此时以
轴,此时以![]() 为直径的圆
为直径的圆![]() 与直线
与直线![]() 相切.
相切.
当![]() 时,则直线
时,则直线![]() 的斜率
的斜率![]() .
.
所以直线![]() 的方程为
的方程为![]() .
.
点![]() 到直线
到直线![]() 的距离
的距离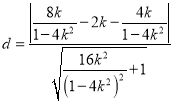
 .
.
又因为![]() ,所以
,所以![]() .
.
故以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
综上得,当直线![]() 绕点
绕点![]() 转动时,以
转动时,以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:![]() (a>0),过点P(-2,-4)的直线l的参数方程为
(a>0),过点P(-2,-4)的直线l的参数方程为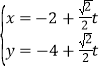 (t为参数),l与C分别交于M,N.
(t为参数),l与C分别交于M,N.
(1)写出C的平面直角坐标系方程和l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,郑州经济快速发展,跻身新一线城市行列,备受全国瞩目.无论是市内的井字形快速交通网,还是辐射全国的米字形高铁路网,郑州的交通优势在同级别的城市内无能出其右.为了调查郑州市民对出行的满意程度,研究人员随机抽取了1000名市民进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中![]() .
.
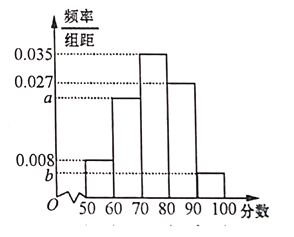
(1)求![]() 的值;
的值;
(2)若按照分层抽样从[50,60),[60,70)中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在[50,60)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学高三文科班学生共有800人参加数学与地理的学业水平测试,从中随机抽取100人的数学与地理的学业水平测试成绩如下表:
人数 | 数学 | |||
优秀 | 良好 | 及格 | ||
地理 | 优秀 | 7 | 20 | 5 |
良好 | 9 | 18 | 6 | |
及格 | a | 4 | b | |
成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩例如:表示数学成绩为良好的共有20+18+4=42(人).
(Ⅰ)若在该样本中,数学成绩优秀率为30%,求a,b的值;
(Ⅱ)已知a≥10,b≥8,利用样本数据,求数学成绩为优秀的人数比及格的人数少的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考![]() 最大的特点就是取消文理分科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这6科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全文(选择政治、历史、地理)的选择是否与性别有关,从某学校高一年级的1000名学生中随机抽取男生,女生各25人进行模拟选科.经统计,选择全文的人数比不选全文的人数少10人.
最大的特点就是取消文理分科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这6科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全文(选择政治、历史、地理)的选择是否与性别有关,从某学校高一年级的1000名学生中随机抽取男生,女生各25人进行模拟选科.经统计,选择全文的人数比不选全文的人数少10人.
(1)估计在男生中,选择全文的概率.
(2)请完成下面的![]() 列联表;并估计有多大把握认为选择全文与性别有关,并说明理由;
列联表;并估计有多大把握认为选择全文与性别有关,并说明理由;
选择全文 | 不选择全文 | 合计 | |
男生 | 5 | ||
女生 | |||
合计 |
附: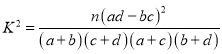 ,其中
,其中![]() .
.
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com