
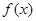 的定义域为
的定义域为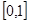 ,且同时满足以下三个条件:①
,且同时满足以下三个条件:①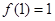 ;②对任意的
;②对任意的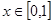 ,都有
,都有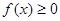 ;③当
;③当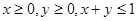 时总有
时总有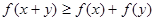 .
.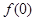 的值;
的值;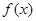 的最大值;
的最大值;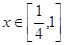 时,恒有
时,恒有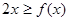 .
.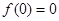 ;(2)
;(2)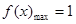 ;(3)
;(3)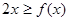 .
.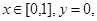 代入抽象函数可得
代入抽象函数可得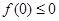 ,又因为
,又因为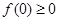 ,可得
,可得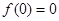 .(2)在定义域内求抽象函数最值,一般先判断函数单调性,再求比较定义域端点的函数值和极值点的大小.证明单调性可令
.(2)在定义域内求抽象函数最值,一般先判断函数单调性,再求比较定义域端点的函数值和极值点的大小.证明单调性可令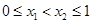 ,代入得
,代入得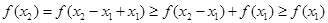 进而得函数为增函数,最大值为
进而得函数为增函数,最大值为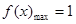 ;
;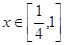 上证不等式
上证不等式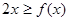 ,要分两段
,要分两段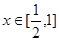 、
、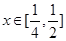 .在
.在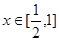 上
上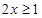 ,
,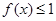 ,所以
,所以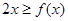 .在
.在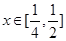
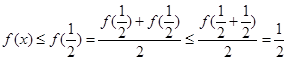 ,
, ,所以
,所以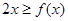 ,进而得证.
,进而得证.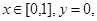 则有
则有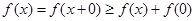 ,所以有
,所以有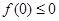 ,有根据条件?可知
,有根据条件?可知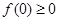 ,故
,故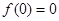 .(也可令
.(也可令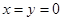 )
)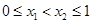 ,则有
,则有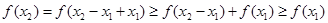 ,即
,即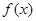 为增函数(严格来讲为不减函数),所以
为增函数(严格来讲为不减函数),所以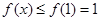 ,故
,故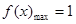 .
.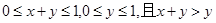 ,所以由?
,所以由? ,即
,即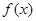 增函数(严格来讲为不减函数),所以
增函数(严格来讲为不减函数),所以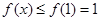 ,故
,故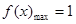 .
.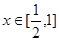 ,有
,有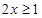 ,又由?可知
,又由?可知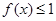 ,所以有
,所以有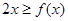 对任意的
对任意的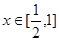 恒成立.当
恒成立.当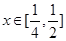 ,又由?可知
,又由?可知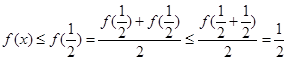 ,所以有
,所以有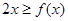 对任意的
对任意的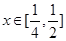 恒成立.综上,对任意的
恒成立.综上,对任意的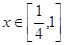 时,恒有
时,恒有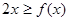 .
.

科目:高中数学 来源:不详 题型:填空题
 是函数
是函数 图象上的任意一点,
图象上的任意一点, 是该图象的两个端点, 点
是该图象的两个端点, 点 满足
满足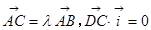 ,(其中
,(其中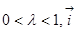 是
是 轴上的单位向量),若
轴上的单位向量),若 (
( 为常数)在区间
为常数)在区间 上恒成立,则称
上恒成立,则称 在区间
在区间 上具有 “
上具有 “ 性质”.现有函数:
性质”.现有函数: ; ②
; ②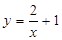 ; ③
; ③ ; ④
; ④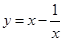 .
. 上具有“
上具有“ 性质”的函数为 .
性质”的函数为 .查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 的定义域为
的定义域为 ,部分对应值如表.
,部分对应值如表. 的导函数
的导函数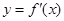 的图象如图所示.下列关于函数
的图象如图所示.下列关于函数 的命题:①函数
的命题:①函数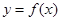 是周期函数;②函数
是周期函数;②函数 在
在 是减函数;③如果当
是减函数;③如果当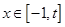 时,
时, 的最大值是2,那么
的最大值是2,那么 的最大值为4;④当
的最大值为4;④当 时,函数
时,函数 有4个零点.其中真命题的个数是 .
有4个零点.其中真命题的个数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com