
����Ŀ����ͼ��ԲO��һ�뾶Ϊ10��Բ�β�ƺ��Ϊ�������ܱ��������㳡�����Ҫ���ֹ滮�ڲ�ƺ�Ͻ�һ���㳡���㳡��״��ͼ�����߲�����ʾ�������ı��Σ�����A��B�����ڡ�O�ϣ�A��B��C��Dǡ��һ�������ε��ĸ����㣮���ݹ滮Ҫ����A��B��C��D�ĵ㴦��װ��յ�����豸����Բ��O��������ڵ�������4����A��B��C��D�ĵ���·OA��OB��OC��OD��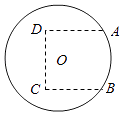
��1���������α߳�Ϊ10�ף���㳡�������
��2���������4����·OA��OB��OC��OD�ܳ��ȵ���Сֵ��
���𰸡�
��1���⣺����AB��
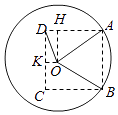
��AB=10����������ABCD�����Ϊ100��
��OA=OB=10�����AOB���������� ![]() ��
��
��Բ�����Ϊ100�У�������AOB�����Ϊ ![]() ��
��
��������AOB�����Ϊ ![]() ��
��
������Ϊ ![]() ��
��
��㳡���Ϊ100+ ![]() ��ƽ���ף���
��ƽ���ף���
��2����O��OK��CD������ΪK����O��OH��AD�������ӳ��ߣ�������ΪH��
���OAD=�ȣ�0���ȣ� ![]() ����
����
��OH=10sin�ȣ�AH=10cos�ȣ�
��DH=|AD��AH|=|2OH��AH|=|20sin�ȩ�10cos��|��
��OD= ![]() =
= ![]() ��
��
�൱��= ![]() ʱ��
ʱ�� ![]() ��
��
�������4����·OA��OB��OC��OD�ܳ��ȵ���СֵΪ ![]() ���ף���
���ף���
����������1�����㳡�������Ϊ�������빭�ε�����ͣ���������������������ȥ�����ε���������㣻��2�������4����·OA��OB��OC��OD��OA��OBΪԲ�İ뾶����OC��OD������ȣ��������OC��OD����Сֵ�������4����·�ܳ��ȵ���Сֵ .
�����㾫�����������⣬������Ҫ�˽�ֱ����Բ������λ�ù�ϵ(ֱ����Բ������λ�ù�ϵ��������Ϊ���룻������������Ϊ�ཻ,����ֱ�߽���Բ�ĸ��ߣ�Բ��ֱ����Ψһ������Ϊ���У�����ֱ�߽���Բ�����ߣ����Ψһ�Ĺ���������е�)��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����Ӱ������S��ij��A����������ǰ��B����һ�����������������O�����Ǻ������ײ�B�ĸ��Ǿ�Ϊ ![]() ����S���۾�������ľ���Ϊ
����S���۾�������ľ���Ϊ ![]() ��
��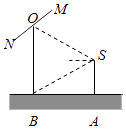
��1������Ӱ�����ߵ�������ˮƽ����������ĸ߶ȣ�
��2�������Ķ�����һ��2�IJʸ�MN�����е�O��S���������ڵ�ƽ������ת����Ӱ��������һ�ӽǷ�ΧΪ ![]() �ľ�ͷ���ڲʸ�ת��������ʱ�̣���Ӱ�������Ƿ��Խ��ʸ�ȫ�����뻭�棿��˵�����ɣ�
�ľ�ͷ���ڲʸ�ת��������ʱ�̣���Ӱ�������Ƿ��Խ��ʸ�ȫ�����뻭�棿��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�����ѧ��ѧϰӢ�����Ȥ���ڰ��ھ���Ӣ��д��˵�����ۺ�����������������ΪԤ���;���2���Σ�Ԥ��Ϊ���ԣ�����Ϊ˵Ӣ���Ӣ������������вμӱ��Ե�ͬѧ����ͳ�ƣ��õ�Ƶ�ʷֲ�ֱ��ͼ�����к��������θ߶�֮������Ϊ4��2��1������[80��90��������Ϊ12�ˣ�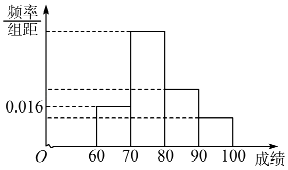
������˰༶������
�����涨Ԥ���ɼ�������90�ֵ�ѡ�ֲμӾ�������֪������λѡ���Ѿ�ȡ�þ����ʸμӾ�����ѡ�ְ���ǩ��ʽ��������˳��
��i���ײ����ڵ�һλ�Ҳ��������һλ�ĸ��ʣ�
��ii���Ǽ��Ҷ�������ǰ��λ������ΪX����X�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ����ΪF1 �� ��һС��A��F1�����ٶ�v��ʼ��ֱ���˶�������Բ�ڷ��䣨���۾������η����ٶȴ�Сʼ�ձ��ֲ��䣬С��뾶���Բ��ƣ�����С���һ�λص�F1ʱ�������õ��ʱ�������ʱ���5��������Բ��������Ϊ��������
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x2+ ![]() +alnx��
+alnx��
������f��x��������[2��3]�ϵ�����������ʵ��a��ȡֵ��Χ��
������f��x���ĵ�����f�䣨x����ͼ��Ϊ����C������C�ϵIJ�ͬ����A��x1 �� y1����B��x2 �� y2������ֱ�ߵ�б��Ϊk����֤����a��4ʱ��|k|��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������A��BCD�У���֪��ABD����BCD���DZ߳�Ϊ2�ĵȱ������Σ�EΪBD�е㣬��AE��ƽ��BCD��FΪ�߶�AB��һ���㣬�� ![]() ��
��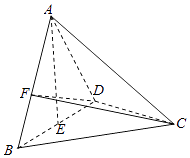
��1���� ![]() ʱ��������ֱ��DF��BC���ɽǵ�����ֵ��
ʱ��������ֱ��DF��BC���ɽǵ�����ֵ��
��2����CF��ƽ��ACD���ɽǵ�����ֵΪ ![]() ʱ����˵�ֵ��
ʱ����˵�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�PA=PB��PA��PB��AB��BC����ƽ��PAB��ƽ��ABCD����AB=2��BC=1�� ![]() ��
��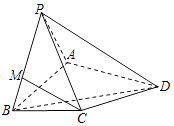
��1����֤��PA��ƽ��PBC��
��2������M����PB�ϣ���PM��MB=3����֤CM��ƽ��PAD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����0��1��2��3��4�����������ѡ������ͬ�������һ����λ������YΪ����ɵ���λ����λ����֮�ͣ�
��1����Y�������ĸ��ʣ�
��2����Y�ĸ��ʷֲ�����ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD�У�M����AD���е㣬O�ǵ�A�ڵ���BCD�ڵ���Ӱ��������ֱ��BM��AO���ɽǵ�����ֵΪ��������
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com