[题目]设F1和F2为双曲线 ﹣ =1的两个焦点.若F1 . F2 . P是正三角形的三个顶点.则双曲线的渐近线方程是( )A.y=± xB.y=± xC.y=± xD.y=± x 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】设F1和F2为双曲线 ﹣ =1（a＞0，b＞0）的两个焦点，若F1 ， F2 ， P（0，2b）是正三角形的三个顶点，则双曲线的渐近线方程是（　　）
A.y=± x
B.y=± x
C.y=± x
D.y=± x

【答案】B
【解析】解：若F1，F2，P（0，2b）是正三角形的三个顶点，

设F1（﹣c，0），F2（c，0），则|F1P|= ，

∵F1、F2、P（0，2b）是正三角形的三个顶点，

∴ =2c，∴c2+4b2=4c2，

∴c2+4（c2﹣a2）=4c2，

∴c2=4a2，即c=2a，

b= = a，

∴双曲线的渐近线方程为y=± x，

即为y=± x．

故答案为：B．

根据F1，F2，P（0，2b）是正三角形的三个顶点，求得c与b的关系式，再结合双曲线中a，b，c三者的关系，即可求得双曲线的渐近线的方程.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】函数f（x）=sin（2x+φ），其中φ为实数，若f（x）≤|f（）|对（0，+∞）恒成立，且，则f（x）的单调递增区间是．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=ln（x+1）﹣x2+（2﹣a）x﹣a（a∈R）若存在唯一的正整数x0 ，使得f（x0）＞0，则实数a的取值范围是（　　）
A.[ ， ]
B.（，）
C.（， ]
D.（ln3，ln2+1）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设全集U=R，集合M={x|x2+x﹣2＞0}，，则（UM）∩N=（　　）
A.[﹣2，0]
B.[﹣2，1]
C.[0，1]
D.[0，2]

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的，其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．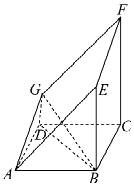

（1）求证：BD⊥平面ADG；
（2）求直线GB与平面AEFG所成角的正弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=2cos2x+2 sinxcosx+a，且当x∈[0， ]时，f（x）的最小值为2．
（Ⅰ）求a 的值；
（Ⅱ）先将函数y=f （x）的图象上点的纵坐标不变，横坐标缩小为原来的，再将所得的图象向右平移个单位，得到函数y=g（x）的图象，求方程g（x）=4在区间[0， ]上所有根之和．