
如图,△ABC中,AC=BC=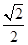 AB,ABED是边长为1的正方形,EB⊥底面ABC,若G,F分别是EC,BD的中点.
AB,ABED是边长为1的正方形,EB⊥底面ABC,若G,F分别是EC,BD的中点.
(1)求证:GF∥底面ABC;
(2)求证:AC⊥平面EBC;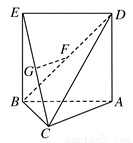
(1)先证明GF//AC,再根据线面平行的判定定理即可证明
(2)先证BE⊥AC,再证AC⊥BC,根据线面垂直的判定定理即可证明
【解析】
试题分析:(1)连接AE,如下图所示.
∵ADEB为正方形,∴AE∩BD=F,且F是AE的中点,
又G是EC的中点,∴GF∥AC,
又AC?平面ABC,GF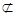 平面ABC,
平面ABC,
∴GF∥平面ABC.
(2)∵ADEB为正方形,∴EB⊥AB,
又∵平面ABED⊥平面ABC,平面ABED∩平面ABC=AB,EB?平面ABED,
∴BE⊥平面ABC,∴BE⊥AC.
又∵AC=BC= AB,∴CA2+CB2=AB2,∴AC⊥BC.
AB,∴CA2+CB2=AB2,∴AC⊥BC.
又∵BC∩BE=B,∴AC⊥平面BCE.
考点:本小题主要考查空间中线面平行与线面垂直的证明,考查学生的空间想象能力.
点评:要证明线面平行与线面垂直,就要紧扣相应的判定定理和性质定理,定理中要求的条件缺一不可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
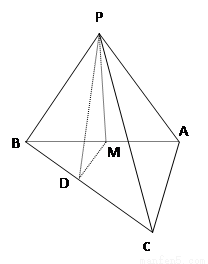
 如图,△ABC中,∠A=90°,AB=4,AC=3,平面ABC外一点P在平面ABC内的射影是AB中点M,二面角P-AC-B的大小为45°.
如图,△ABC中,∠A=90°,AB=4,AC=3,平面ABC外一点P在平面ABC内的射影是AB中点M,二面角P-AC-B的大小为45°.查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| AD |
| AB |
| AE |
| AC |
| 1 |
| 2 |
| π |
| 6 |

查看答案和解析>>
科目:高中数学 来源:2014届黑龙江大庆实验中学高二上学期开学考试理科数学试卷(解析版) 题型:解答题
(本题满分12分)如图,ΔABC中,∠A=90°,AB=4,AC=3,平面ABC外一点P在平面ABC内的射影是AB中点M,二面角P—AC—B的大小为45°.
(I)求二面角P—BC—A的正切值;
(II)求二面角C—PB—A的正切值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年黑龙江省大庆实验中学高二(上)期初数学试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com