
【题目】已知函数f(x)=|2x﹣a|+|x﹣1|,a∈R.
(Ⅰ)若不等式f(x)≥2﹣|x﹣1|恒成立,求实数a的取值范围;
(Ⅱ)当a=1时,直线y=m与函数f(x)的图象围成三角形,求m的最大值及此时围成的三角形的面积.
【答案】解:(I)∵f(x)≥2﹣|x﹣1|恒成立,即|x﹣ ![]() |+|x﹣1|≥1恒成立, 又|x﹣
|+|x﹣1|≥1恒成立, 又|x﹣ ![]() |+|x﹣1|≥|x﹣
|+|x﹣1|≥|x﹣ ![]() ﹣(x﹣1)|=|1﹣
﹣(x﹣1)|=|1﹣ ![]() |,
|,
∴|1﹣ ![]() |≥1,解得a≤0或a≥4.
|≥1,解得a≤0或a≥4.
∴a的取值范围是(﹣∞,0]∪[4,+∞).
(II)当a=1时,f(x)=|2x﹣1|+|x﹣1|=  ,
,
做出f(x)的函数图象如图所示:
由图象可知当 ![]() <m≤1时,直线y=m与f(x)的图象构成三角形.
<m≤1时,直线y=m与f(x)的图象构成三角形.
∴m的最大值为1,
令2﹣3x=1得x= ![]() ,此时围成三角形的面积为
,此时围成三角形的面积为 ![]() (1﹣
(1﹣ ![]() )×(1﹣
)×(1﹣ ![]() )=
)= ![]()
【解析】(I)利用绝对值三角不等式得出|x﹣ ![]() |+|x﹣1|的最小值,从而解出a的范围;(II)做出f(x)的函数图象,根据函数图象得出m的范围.
|+|x﹣1|的最小值,从而解出a的范围;(II)做出f(x)的函数图象,根据函数图象得出m的范围.
【考点精析】根据题目的已知条件,利用绝对值不等式的解法的相关知识可以得到问题的答案,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


科目:高中数学 来源: 题型:
【题目】
为了保护环境,发展低碳经济,某单位在政府部门的支持下,进行技术攻关,采用了新工艺,新上了把二氧化碳转化为一种可利用的化工产品的项目.经测算,月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可以近似的表示为:
(吨)之间的函数关系可以近似的表示为: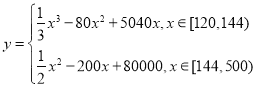 ,且每处理一吨二氧化碳可得到能利用的化工产品价值为200元,若该项目不获利,政府将补贴.
,且每处理一吨二氧化碳可得到能利用的化工产品价值为200元,若该项目不获利,政府将补贴.
(I)当![]() 时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损;
时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损;
(II)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() .
.
(1)若a、b是一枚骰子掷两次所得到的点数,求方程有两正根的概率;
(2)若a∈[2,4],b∈[0,6],求方程没有实根的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的右焦点为F,不垂直x轴且不过F点的直线l与椭圆C相交于A,B两点.
的右焦点为F,不垂直x轴且不过F点的直线l与椭圆C相交于A,B两点.
(Ⅰ)若直线l经过点P(2,0),则直线FA、FB的斜率之和是否为定值?若是,求出该定值;若不是,请说明理由;
(Ⅱ)如果FA⊥FB,原点到直线l的距离为d,求d的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了考查两个变量![]() 和
和![]() 之间的线性关系,甲、乙两位同学各自独立作了
之间的线性关系,甲、乙两位同学各自独立作了![]() 次和
次和![]() 次试验,并且利用线性回归方法,求得回归直线分别为
次试验,并且利用线性回归方法,求得回归直线分别为![]() 、
、![]() ,已知两人得的试验数据中,变量
,已知两人得的试验数据中,变量![]() 和
和![]() 的数据的平均值都相等,且分别都是
的数据的平均值都相等,且分别都是![]() 、
、![]() ,那么下列说法正确的是( )
,那么下列说法正确的是( )
A. 直线![]() 和
和![]() 一定有公共点
一定有公共点![]() B. 必有直线
B. 必有直线![]()
C. 直线![]() 和
和![]() 相交,但交点不一定是
相交,但交点不一定是![]() D.
D. ![]() 和
和![]() 必定重合
必定重合
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax﹣x2﹣lnx存在极值,若这些极值的和大于5+ln2,则实数a的取值范围为( )
A.(﹣∞,4)
B.(4,+∞)
C.(﹣∞,2)
D.(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区工会利用“健步行![]() ” 开展健步走积分奖励活动.会员每天走5 千步可获积分30分(不足5千步不积分), 每多走2千步再积20分(不足2千步不积分).为了解会员的健步走情况,工会在某天从系统中随机抽取了 1000名会员,统计了当天他们的步数,并将样本数据分为
” 开展健步走积分奖励活动.会员每天走5 千步可获积分30分(不足5千步不积分), 每多走2千步再积20分(不足2千步不积分).为了解会员的健步走情况,工会在某天从系统中随机抽取了 1000名会员,统计了当天他们的步数,并将样本数据分为![]() ,
,![]() 九组,整理得到如图频率分布直方图:
九组,整理得到如图频率分布直方图:
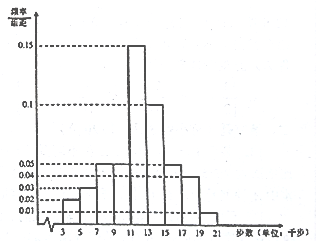
(1)求当天这1000名会员中步数少于11千步的人数;
(2)从当天步数在![]() 的会员中按分层抽样的方式抽取6人,再从这6人中随机抽取2人,求这2人积分之和不少于200分的概率;
的会员中按分层抽样的方式抽取6人,再从这6人中随机抽取2人,求这2人积分之和不少于200分的概率;
(3)写出该组数据的中位数(只写结果).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (α为参数),直线C2的方程为y=
(α为参数),直线C2的方程为y= ![]() ,以O为极点,以x轴正半轴为极轴建立极坐标系,
,以O为极点,以x轴正半轴为极轴建立极坐标系,
(1)求曲线C1和直线C2的极坐标方程;
(2)若直线C2与曲线C1交于A,B两点,求 ![]() +
+ ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com