
科目:高中数学 来源:2017届江苏扬州中学等七校高三上期中联考数学试卷(解析版) 题型:解答题
如图,某广场中间有一块边长为2百米的菱形状绿化区ABCD,其中BMN是半径为1百米的扇形,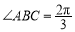 .管理部门欲在该地从M到D修建小路:在
.管理部门欲在该地从M到D修建小路:在 上选一点P(异于M、N两点),过点P修建与BC平行的小路PQ.
上选一点P(异于M、N两点),过点P修建与BC平行的小路PQ.

(1)若 ,求
,求 的长度;
的长度;
(2)当点P选择在何处时,才能使得修建的小路 与PQ及QD的总长最小?并说明理由.
与PQ及QD的总长最小?并说明理由.
查看答案和解析>>
科目:高中数学 来源:2017届贵州遵义市高三上期中数学(理)试卷(解析版) 题型:解答题
选修4-5:不等式选讲
已知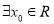 使不等式
使不等式 成立.
成立.
(1)求满足条件的实数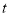 的取值集合
的取值集合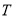 ;
;
(2)若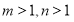 ,对
,对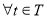 ,不等式
,不等式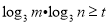 恒成立,求
恒成立,求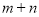 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2017届贵州遵义市高三上期中数学(理)试卷(解析版) 题型:选择题
已知 ,给出下列四个结论:
,给出下列四个结论:
①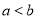 ②
②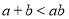 ③
③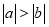 ④
④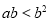
其中正确结论的序号是( )
A.①② B.②③ C.②④ D.③④
查看答案和解析>>
科目:高中数学 来源:2016-2017学年江苏清江中学高二上期中数学试卷(解析版) 题型:解答题
已知圆C1: 与y轴交于O,A两点,圆C2过O,A两点,且直线C2O恰与圆C1相切;
与y轴交于O,A两点,圆C2过O,A两点,且直线C2O恰与圆C1相切;

(1)求圆C2的方程。
(2)若圆C2上一动点M,直线MO与圆C1的另一交点为N,在平面内是否存在定点P使得PM=PN始终成立,若存在,求出定点坐标,若不存在,说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com