
【题目】(2015·陕西)“sin![]() =cos
=cos![]() ”是“cos2
”是“cos2![]() =0”的( )
=0”的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
【题目】![]() 在直角坐标系xOy中,曲线C1:
在直角坐标系xOy中,曲线C1:![]() (t为参数,且t≠0),其中0
(t为参数,且t≠0),其中0![]()
![]()
![]() , 在以O为极点x轴正半轴为极轴的极坐标系中,曲线C2::
, 在以O为极点x轴正半轴为极轴的极坐标系中,曲线C2::![]() =2sin
=2sin![]() , C3:
, C3:![]() =2
=2![]() cos
cos![]()
(1)求C2与C3交点的直角坐标
(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)设直线l与抛物线y2=4x相交于A,B两点,与圆(x-5)2+y2=r2(r>0)相切于点M,且M为线段AB的中点.若这样的直线l恰有4条,则r的取值范围是( )
A.(1,3)
B.(1, 4)
C.(2,3)
D.(2,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)如图,A , B , C , D为平面四边形ABCD的四个内角.
(1)证明:tan![]() =
=![]()
(2)若A+C=180°, AB=6, BC=3, CD=4, AD=5, 求tan![]() +tan
+tan![]() +tan
+tan![]() +tan
+tan![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)如图,椭圆E:![]() (a>b>0)经过点A(0,-1),且离心率为
(a>b>0)经过点A(0,-1),且离心率为![]() .
.
(1)求椭圆E的方程;
(2)经过点(1,1),且斜率为k的直线与椭圆E交于不同两点P,Q(均异于点A),证明:直线AP与AQ的斜率之和为2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)如图1,在直角梯形ABCD中,AD∥BC,![]() BAD=
BAD=![]() ,AB=BC=1,
,AB=BC=1,
AD=2, E是AD的中点,0是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图2.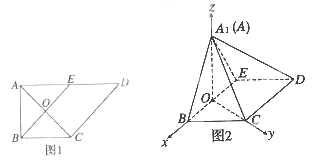
(1)证明:CD⊥平面A1OC
(2)若平面A1BE⊥平面BCDE, 四棱锥A1-BCDE的体积为36![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·江苏) 已知函数f(x)=x3+ax2+b(a,b![]() R).
R).
(1)试讨论f(x)的单调性;
(2)若b=c-a(实数c是a与无关的常数),当函数f(x)有三个不同的零点时,a的取值范围恰好是(-![]() ,-3)
,-3)![]() (1,
(1,![]() )
)![]() (
(![]() ,+
,+![]() ),求c的值.
),求c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若n是一个三位正整数,且n的个位数字大于十位数字,十位数字大于百位数字,则称n为“三位递增数”(如137,359,567等).在某次数学趣味活动中,每位参加者需从所有的“三位递增数”中随机抽取1个数,且只能抽取一次.得分规则如下:若抽取的“三位递增数”的三个数字之积不能被5整除,参加者得0分;若能被5整除,但不能被10整除,得-1分;若能被10整除,得1分.
(1)写出所有个位数字是5的“三位递增数” ;
(2)若甲参加活动,求甲得分X的分布列和数学期望EX.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com