
(本题满分12分)
甲、乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,
答错得零分.假设甲队中每人答对的概率均为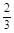 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为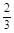 ,
,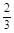 ,
, ,且各人回答正确与否相互之间没有影响.用
,且各人回答正确与否相互之间没有影响.用 表示甲队的总得分.
表示甲队的总得分.
(1)求 的概率及
的概率及 的数学期望
的数学期望 ;
;
(2)用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分”这一事件,求 .
.
(1)E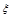 =2;(2)P(AB) =
=2;(2)P(AB) =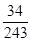
【解析】本题考查相互独立重复事件的概率计算,离散变量的分步列、期望的计算,解题时要明确事件之间的关系并准确计算.
(Ⅰ)因为假设甲队中每人答对的概率均为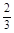 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为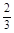 ,
,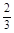 ,
,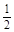 ,且各人回答正确与否相互之间没有影响,结合独立事件概率的乘法公式得到结论。
,且各人回答正确与否相互之间没有影响,结合独立事件概率的乘法公式得到结论。
(Ⅱ)由题意,ξ可取的值为0、1、2、3,由n次独立重复实验中恰有k次发生的概率公式计算P(ξ=0)、P(ξ=1)、P(ξ=3)、P(ξ=4),进而可得ξ的分步列,进而由期望公式,计算可得答案.
解 (1)方法一 由题意知,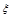 的可能取值为0,1,2,3,且
的可能取值为0,1,2,3,且
P(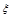 =0)=
=0)=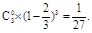 ,P(
,P(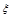 =1)=
=1)=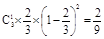 ,
,
P(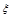 =2)=
=2)=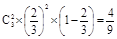 ,P(
,P(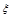 =3)=
=3)=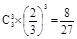 .
.
所以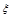 的分布列为
的分布列为
|
|
0 |
1 |
2 |
3 |
|
P |
|
|
|
|
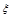 的数学期望为E
的数学期望为E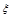 =0×
=0×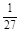 +1×
+1×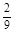 +2×
+2×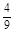 +3×
+3×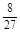 =2.
=2.
方法二
根据题设可知, 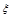 ~B
~B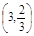 ,
,
故P(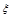 =1)=
=1)=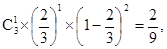
因为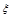 ~B
~B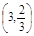 ,所以E
,所以E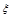 =3×
=3×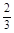 =2.--------------------6分
=2.--------------------6分
(2)方法一 用C表示“甲队得2分乙队得1分”这一事件,用D表示“甲队得3分乙队得0分”这一事件,所以AB=C∪D,且C、D互斥,
P(C)=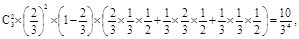 P(D)=
P(D)=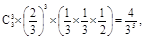
由互斥事件的概率公式得P(AB)=P(C)+P(D)=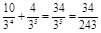 .
.
方法二 用Ak表示“甲队得k分”这一事件,用Bk表示“乙队得k分”这一事件,k=0,1,2,3.由于事件A3B0,A2B1为互斥事件,故有P(AB)=P(A3B0∪A2B1)=P(A3B0)+P(A2B1).由题设可知,事件A3与B0独立,事件A2与B1独立,因此
P(AB)=P(A3B0)+P(A2B1)=P(A3)P(B0)+P(A2)P(B1)
=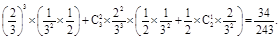 ---------------------12分
---------------------12分


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:高中数学 来源: 题型:
| π | 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年上海市金山区高三上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分12分,第1小题6分,第2小题6分)
已知集合A={x| | x–a | < 2,xÎR
},B={x| <1,xÎR }.
<1,xÎR }.
(1) 求A、B;
(2) 若 ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省高三10月月考理科数学试卷(解析版) 题型:解答题
(本题满分12分)
设函数 (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
.
(1)求 的解析式;
的解析式;
(2)证明:曲线 的图像是一个中心对称图形,并求其对称中心.
的图像是一个中心对称图形,并求其对称中心.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆市高三第二次月考文科数学 题型:解答题
(本题满分12分,(Ⅰ)小问4分,(Ⅱ)小问6分,(Ⅲ)小问2分.)
如图所示,直二面角 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
(Ⅰ)求证: ⊥平面
⊥平面
(Ⅱ)求二面角 的大小;
的大小;
(Ⅲ)求点 到平面
到平面 的距离.
的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com