练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆和双曲线有共同焦点，是它们的一个交点，，记椭圆和双曲线的离心率分别，则的最小值是（ ）

    A. B. C. D.

    【答案】A

    【解析】

    由题意设焦距为2c，椭圆长轴长为2a，双曲线实轴为2m，令P在双曲线的右支上，由已知条件结合双曲线和椭圆的定义，以及余弦定理推出a2+3m2=4c2，进而求出e12+e22的最小值

    由题意设焦距为2c，椭圆长轴长为2a，双曲线实轴为2m，

    令P在双曲线的右支上，由双曲线的定义|PF1|-|PF2|=2m，由椭圆定义|PF1|+|PF2|=2a，

    可得|PF1|=m+a，|PF2|=a-m，又∠F1PF2＝60°，

    根据余弦定理得 ：|PF1|2+|PF2|2-|PF1||PF2|=4c2，

    可得（m+a）2+（a-m）2-（m+a）（a-m）=4c2，整理得a2+3m2=4c2，

    即 ，可得 ，

    则

    当且仅当时，取等号，故选A .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆上存在关于直线对称的相异两点，则实数的取值范围是____．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列{an}的前n项和为Sn.已知2Sn＝3n＋3.

    (1)求{an}的通项公式；

    (2)若数列{bn}满足anbn＝log3an，求{bn}的前n项和Tn.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设x≥1，y≥1，证明：x＋y＋≤＋xy.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】当曲线与直线有两个相异的交点时,实数的取值范围是 （ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若x=﹣2是函数f（x）=（x2+ax﹣1）ex﹣1的极值点，则f（x）的极小值为（ ）
    A.﹣1
    B.﹣2e﹣3
    C.5e﹣3
    D.1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中，底面为正三角形，侧棱底面．已知是 的中点，．

    （1）求证：平面平面；

    （2）求证：A1C∥平面；

    （3）求三棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥P-ABC中， 且底面，D是PC的中点，已知,AB=2，AC=,PA=2.

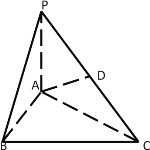
    （1）求三棱锥P-ABC的体积

    （2）求异面直线BC与AD所成角的余弦值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题中是真命题的个数是（ ）

    （1）垂直于同一条直线的两条直线互相平行

    （2）与同一个平面夹角相等的两条直线互相平行

    （3）平行于同一个平面的两条直线互相平行

    （4）两条直线能确定一个平面

    （5）垂直于同一个平面的两个平面平行

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案