
���� ��1��������к���������жϣ�1����
��2�����������ϲ�ȡ�����жϣ�2����
��3��д���ֶκ������ֵ���жϣ�3����
��4��������Ǻ����ĶԳ������жϣ�4����
��5������֪����ʵ��x1��x2��ʹ�ö������ʵ��x����f��x1����f��x����f��x2������ת��Ϊ�����������жϣ�5����
��� �⣺��1����tanx=0����x=k�У�k��Z���ຯ��f��x��=tanx����������㣬�ʣ�1����ȷ��
��2������A={x|y=2x+1}=R������ B={x|y=x2+x+1}=R����A��B=R���ʣ�2������
��3������$f��x��=\frac{1}{2}sinx+\frac{1}{2}|{sinx}|$=$\left\{\begin{array}{l}{sinx��sinx��0}\\{0��sinx��0}\end{array}\right.$����ֵ����[0��1]���ʣ�3������
��4����2x+$\frac{��}{3}=k��$����x=$\frac{k��}{2}-\frac{��}{6}$��k��Z��ȡk=1����x=$\frac{��}{3}$���ຯ��$f��x��=2sin��2x+\frac{��}{3}��$��ͼ���һ���Գ�����Ϊ$��\frac{��}{3}��0��$���ʣ�4����ȷ��
��5���ߺ���f��x��=2cosx������Ϊ2�У�����ʵ��x1��x2��ʹ�ö������ʵ��x����f��x1����f��x����f��x2��������˵��|x1-x2|����СֵΪ$\frac{1}{2}$����=�У��ʣ�5������
����ȷ�������ǣ�1������4����
�ʴ�Ϊ����1����4����
���� ���⿼�����������ж���Ӧ�ã��������Ǻ�����ͼ������ʣ������������������������������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{3}}{2}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{\sqrt{2}}{8}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �٢� | C�� | �٢� | D�� | �ۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��-2����f��1����f��3�� | B�� | f��1����f��-2����f��3�� | C�� | f��3����f��-2����f��1�� | D�� | f��-2����f��3����f��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ij��ѧ����ѧ��������ڼ����ٲμ�һ����ṫ�������¼�ƻ������У��ѧ�繲��100��ѧ�������Dzμӻ�Ĵ���ͳ����ͼ��ʾ�������ѧ��������ѡ1��ѧ�������μӻ����Ϊ3�ĸ����ǣ�������
ij��ѧ����ѧ��������ڼ����ٲμ�һ����ṫ�������¼�ƻ������У��ѧ�繲��100��ѧ�������Dzμӻ�Ĵ���ͳ����ͼ��ʾ�������ѧ��������ѡ1��ѧ�������μӻ����Ϊ3�ĸ����ǣ�������| A�� | $\frac{1}{10}$ | B�� | $\frac{3}{10}$ | C�� | $\frac{6}{10}$ | D�� | $\frac{7}{10}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
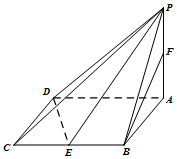 ������P-ABCD�У�����ABCD�DZ߳�Ϊ2�����Σ���BAD=60�㣬PA����ABCD��PA=$\sqrt{3}$��E��F�ֱ�ΪBC��PA���е㣮
������P-ABCD�У�����ABCD�DZ߳�Ϊ2�����Σ���BAD=60�㣬PA����ABCD��PA=$\sqrt{3}$��E��F�ֱ�ΪBC��PA���е㣮�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com