
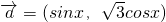 ,
,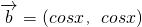 .
. (0<x<
(0<x< ),求tanx的值;
),求tanx的值; 的最小正周期和函数在
的最小正周期和函数在 的最大值及相应x的值.
的最大值及相应x的值.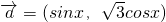 ,
,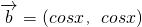 ,
, ,∴sinxcosx-
,∴sinxcosx- cos2x=0.
cos2x=0. ,∴sinx-
,∴sinx- cosx=0,tanx=
cosx=0,tanx=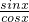 =
= .
. =sinxcosx-
=sinxcosx- cos2x=
cos2x=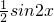 +
+ cos2x+
cos2x+
 )+
)+ ,故它的最小正周期为
,故它的最小正周期为 =π.
=π. ,可得 2x+
,可得 2x+ ∈(
∈( ,
, ),
), =
= 时,函数取得最大值为
时,函数取得最大值为 ,此时,x=
,此时,x= .
. cos2x=0,再由 0<x<
cos2x=0,再由 0<x< ,以及同角三角函数的基本关系求得tanx的值.
,以及同角三角函数的基本关系求得tanx的值. )+
)+ ,由此求得它的最小正周期.再根据正弦函数的定义域和值域,求得函数的最大值.
,由此求得它的最小正周期.再根据正弦函数的定义域和值域,求得函数的最大值.

科目:高中数学 来源:2011年广东省揭阳一中高二第一次阶段性测试题文科数学 题型:解答题
(本小题满分14分)已知ΔABC的角A、B、C所对的边分别是a、b、c,设向量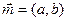 ,
,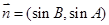 ,
,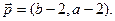
(1)若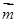 //
//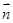 ,求证:ΔABC为等腰三角形;
,求证:ΔABC为等腰三角形;
(2)若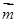 ⊥
⊥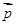 ,边长c = 2,角C =
,边长c = 2,角C = 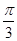 ,求ΔABC的面积 .
,求ΔABC的面积 .
查看答案和解析>>
科目:高中数学 来源:2009年普通高等学校招生全国统一考试文科数学(上海卷) 题型:解答题
(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知 的角
的角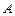 、
、 、
、 所对的边分别是
所对的边分别是 、
、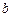 、
、 ,设向量
,设向量 ,
,
 ,
, .
.
(1)若 ,求证:
,求证: 为等腰三角形;
为等腰三角形;
(2)若 ,边长
,边长 ,角
,角 ,求
,求 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏盐城第一中学高三第二学期期初检测文科数学试卷(解析版) 题型:解答题
在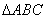 中,角
中,角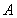 、
、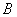 、
、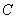 的对边分别为
的对边分别为 、
、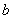 、
、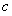 .设向量
.设向量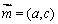 ,
,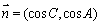 .
.
(1)若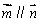 ,
,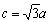 ,求角
,求角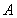 ;(2)若
;(2)若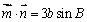 ,
,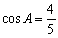 ,求
,求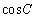 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省高州市高三上学期16周抽考数学理卷 题型:解答题
(13分)已知△ABC的角A.B.C所对的边分别是a.b.c,设向量 ,
, ,
,
(1)若 ,求证△ABC为等腰三角形;
,求证△ABC为等腰三角形;
(2)若 ,边长
,边长 ,角
,角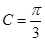 ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com