
 .
. 的区间(a,b),使x∈(a,b);如果没有,请说明理由.
的区间(a,b),使x∈(a,b);如果没有,请说明理由.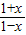 =(
=( ) -1可得f(-x)=-f(x),从而得到函数为奇函数;
) -1可得f(-x)=-f(x),从而得到函数为奇函数; =x-k即k=x-
=x-k即k=x-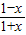 在(-1,1)内有解,从而得出实数k属于函数y=x-
在(-1,1)内有解,从而得出实数k属于函数y=x-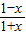 =x+1-
=x+1-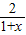 在(-1,1)内的值域.下面利用换元法求出其值域即可得到实数k的取值范围;
在(-1,1)内的值域.下面利用换元法求出其值域即可得到实数k的取值范围; -x-1(-1<x<1).用“二分法”逐步探求,先算区间(-1,1)的中点g(0)=-1<0,由于g(x)在(-1,1)内单调递减,于是再算区间(-1,0)的中点g(-
-x-1(-1<x<1).用“二分法”逐步探求,先算区间(-1,1)的中点g(0)=-1<0,由于g(x)在(-1,1)内单调递减,于是再算区间(-1,0)的中点g(- )=log23-
)=log23- >0,然后算区间(-
>0,然后算区间(- ,0)的中点 g(-
,0)的中点 g(- )<0,最后算区间(-
)<0,最后算区间(- ,-
,- )的中点g(-
)的中点g(- )>0.
)>0. 得-1<x<1,所以函数f(x)的定义域为(-1,1); (2')
得-1<x<1,所以函数f(x)的定义域为(-1,1); (2') +log2
+log2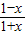 =log2
=log2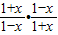 =log21=0,
=log21=0, =x-k即k=x-
=x-k即k=x- 在(-1,1)内有解,
在(-1,1)内有解, =x+1-
=x+1-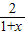 在(-1,1)内的值域. (6')
在(-1,1)内的值域. (6') 在(0,2)内单调递增,所以t-
在(0,2)内单调递增,所以t- ∈(-∞,1).
∈(-∞,1). -x-1(-1<x<1).
-x-1(-1<x<1).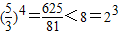 ,且y=log2x在区间(0,+∞)内单调递增,所以log2
,且y=log2x在区间(0,+∞)内单调递增,所以log2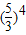 <log223,
<log223, <3,亦即log2
<3,亦即log2 <
< .
. )=log2
)=log2 -
- <0. ①(10')
<0. ①(10') )=log2
)=log2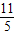 -
- >1-
>1- >0. ②(12')
>0. ②(12') )•g(-
)•g(- )<0,
)<0, ,-
,- )内有零点x.
)内有零点x. ,-
,- )内有实根x. (13')
)内有实根x. (13') ,因此,所求的一个区间可以是(-
,因此,所求的一个区间可以是(- ,-
,- ).(答案不唯一) (14')
).(答案不唯一) (14')

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2(x-1) |
| x+1 |
| x1+x2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| f(n) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| a |
| ||
| x |
| 6 |
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com