
【题目】已知a,b,c均为正数,设函数f(x)=|x﹣b|﹣|x+c|+a,x∈R.
(1)若a=2b=2c=2,求不等式f(x)<3的解集;
(2)若函数f(x)的最大值为1,证明:![]() .
.
【答案】(1)![]() .(2)见解析
.(2)见解析
【解析】
(1)根据a=2b=2c=2时,将不等式f(x)<3化为|x﹣1|﹣|x+1|<1,然后利用零点分段法解不等式即可;
(2)根据条件利用绝对值三角不等式,可得a+b+c=1,然后利用柯西不等式,即可证明![]() .
.
(1)当a=2b=2c=2时,a=2,b=c=1
不等式f(x)<3化为|x﹣1|﹣|x+1|<1,
当x≤﹣1时,原不等式化为1﹣x+1+x<1,解集为;
当﹣1<x<1时,原不等式化为1﹣x﹣x﹣1<1,解得![]() ;
;
当x≥1时,原不等式化为x﹣1﹣x﹣1<1,解得x≥1,
∴不等式f(x)<3的解集为![]() .
.
(2)∵![]()
又∵a,b,c>0,
∴![]()
∴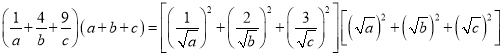
![]()
![]()
当且仅当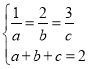 ,即
,即![]() 时等号成立,
时等号成立,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]()
![]() ,点
,点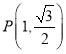 满足:
满足:![]() ,且
,且![]() .
.
(1)求椭圆C的标准方程;
(2)过点![]() 的直线l与C交于
的直线l与C交于![]() ,
,![]() 不同的两点,且
不同的两点,且![]() ,问在x轴上是否存在定点N,使得直线
,问在x轴上是否存在定点N,使得直线![]() ,
,![]() 与y轴围成的三角形始终为底边在y轴上的等腰三角形.若存在,求定点N的坐标;若不存在,请说明理由.
与y轴围成的三角形始终为底边在y轴上的等腰三角形.若存在,求定点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子有5个不同的小球,编号分别为1,2,3,4,5,从袋中一次取出三个球,记随机变量![]() 是取出球的最大编号与最小编号的差,数学期望为
是取出球的最大编号与最小编号的差,数学期望为![]() ,方差为
,方差为![]() 则下列选项正确的是( )
则下列选项正确的是( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯,由此催生了一批外卖点餐平台.已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取100名点外卖的用户进行统计,按送餐距离分类统计结果如表:
送餐距离(千米) | (0,1] | (1,2] | (2,3] | (3,4] | (4,5] |
频数 | 15 | 25 | 25 | 20 | 15 |
以这100名用户送餐距离位于各区间的频率代替送餐距离位于该区间的概率.
(1)若某送餐员一天送餐的总距离为100千米,试估计该送餐员一天的送餐份数;(四舍五入精确到整数,且同一组中的数据用该组区间的中点值为代表).
(2)若该外卖平台给送餐员的送餐费用与送餐距离有关,规定2千米内为短距离,每份3元,2千米到4千米为中距离,每份7元,超过4千米为远距离,每份12元.记X为送餐员送一份外卖的收入(单位:元),求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①:在平行四边形![]() 中,
中,![]() ,
,![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起,使
折起,使![]() ,连结
,连结![]() ,得到如图②所示三棱锥
,得到如图②所示三棱锥![]() .
.
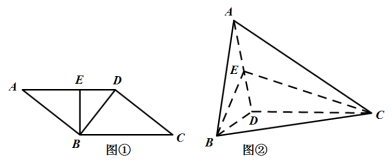
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,二面角
,二面角![]() 的平面角的正切值为
的平面角的正切值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市对一项惠民市政工程满意程度(分值:![]() 分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):
分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):

现用分层抽样的方法从所有参与网上投票的市民中随机抽取![]() 位市民召开座谈会,其中满意程度在
位市民召开座谈会,其中满意程度在![]() 的有5人.
的有5人.
(1)求![]() 的值,并填写下表(2000位参与投票分数和人数分布统计);
的值,并填写下表(2000位参与投票分数和人数分布统计);
满意程度(分数) |
|
|
|
|
|
人数 |
(2)求市民投票满意程度的平均分(各分数段取中点值);
(3)若满意程度在![]() 的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.
的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高铁是我国国家名片之一,高铁的修建凝聚着中国人的智慧与汗水.如图所示,B、E、F为山脚两侧共线的三点,在山顶A处测得这三点的俯角分别为![]() 、
、![]() 、
、![]() ,计划沿直线BF开通穿山隧道,现已测得BC、DE、EF三段线段的长度分别为3、1、2.
,计划沿直线BF开通穿山隧道,现已测得BC、DE、EF三段线段的长度分别为3、1、2.

(1)求出线段AE的长度;
(2)求出隧道CD的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com