
(本小题满分12分)
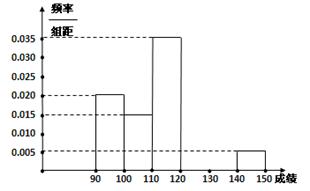
某校高三数学竞赛初赛考试后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六 组,第一组
组,第一组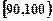 、第二组
、第二组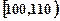 …第六组
…第六组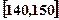 . 如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
. 如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
(Ⅰ)请补充完整频率分布直方图,并估
计这组数据的平均数M;
(Ⅱ)现根据初赛成绩从第四组和第六组
中任意选2人,记他们的成绩分别
为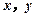 . 若
. 若 ,则称此二
,则称此二
人为“黄金帮扶组”,试求选出的二
人错误!链接无效。的概率 ;
;
(Ⅲ)以此样本的频率当作概率,现随机在这组样本中选出的3名学生,求成绩不低于
120分的人数 分布列及期望
分布列及期望 .
.
科目:高中数学 来源: 题型:解答题
(12分)某班同学利用暑期进行社会实践,对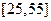 岁的人群随机抽取
岁的人群随机抽取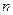 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:

(Ⅰ)补全频率分布直方图并求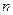 、
、 、
、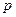 的值;
的值;
(Ⅱ)从年龄段在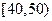 的“低碳族”中采用分层抽样法抽取
的“低碳族”中采用分层抽样法抽取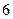 人参加户外低碳体验活动,其中选取
人参加户外低碳体验活动,其中选取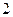 人作为领队,求选取的
人作为领队,求选取的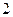 名领队中恰有1人年龄在
名领队中恰有1人年龄在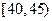 岁的概率。
岁的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量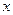 (吨)与相应的生产能耗
(吨)与相应的生产能耗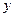 (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
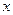 | 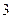 | 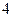 | 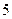 | 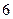 |
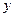 | 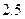 | 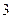 | 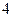 | 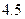 |
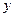 关于
关于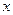 的线性回归方程
的线性回归方程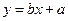 ;
; (参考数值:
(参考数值: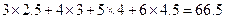 ,
,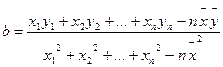 ,
, )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:克),重量的分组区间为(490,495],(495,500],……,(510,515],由此得到样本的频率分布直方图,如图4所示.根据频率分布直方图,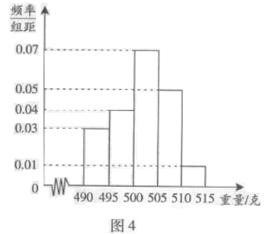
求(1)重量超过500 克的产品的频率;
(2)重量超过500 克的产品的数量.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)班主任为了对本班学生的考试成绩进行分析,决定从全班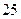 位女同学,
位女同学, 位男同学中随机抽取一个容量为
位男同学中随机抽取一个容量为 的样本进行分析。
的样本进行分析。
(Ⅰ)如果按性别比例分层抽样,可以得到多少个不同的样本(只要求写出算式即可,不必计算出结果);
(Ⅱ)随机抽取 位同学,数学成绩由低到高依次为:
位同学,数学成绩由低到高依次为: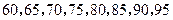 ;
;
物理成绩由低到高依次为: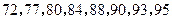 ,若规定
,若规定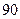 分(含
分(含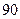 分)以
分)以 上为优秀,记
上为优秀,记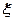 为这
为这 位同学中数学和物理分数均为优秀的人数,求
位同学中数学和物理分数均为优秀的人数,求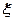 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)若这 位同学的数学、物理分数事实上对应下表:
位同学的数学、物理分数事实上对应下表:
| 学生编号 | 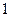 |  | 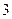 | 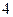 | 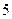 |  | 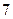 |  |
数学分数 | 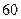 |  | 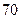 |  | 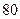 | 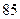 | 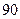 |  |
物理分数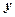 | 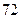 | 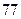 | 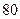 | 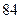 | 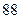 | 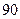 | 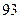 |  |
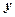 与
与
 之间具有较强的线性相关关系,求出
之间具有较强的线性相关关系,求出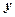 与
与 的线性回归方程(系数精确到
的线性回归方程(系数精确到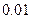 ).(参考公式:
).(参考公式: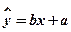 ,其中
,其中 ,
,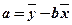 ; 参考数据:
; 参考数据: ,
,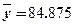 ,
,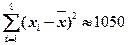 ,
, ,
, ,
,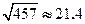 ,
,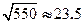 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分8分)
为了了解某校高一学生体能情况,抽取200位同学进行1分钟跳绳次数测试,将所得数据整理后画出频率分布直方图(如图所示),请回答下列问题: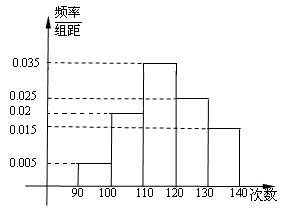
(1)次数在100~110之间的频率是多少?
(2)若次数在110以上为达标,试估计该校全体高一学生的达标率是多少?
(3)根据频率分布直方图估计,学生跳绳次数的平均数是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题14分) 高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
| 分组 | 频数 | 频率 |
 | ① | 0. 025 |
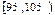 | | 0.050 |
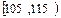 | | 0.200 |
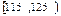 | 12 | 0.300 |
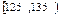 | | 0.275 |
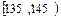 | 4 | ② |
| [145,155] | | 0.050 |
| 合计 | | ③ |
|
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)为研究我校高二年级的男生身高,随机抽取40名男生,实测身高数据(单位:厘米)如下:
171 173 163 169 166 167 168.5 160 170 165
175 169 167 156 165.5 168 170 184 168 174
165 170 174 161 177 175.5 173 164 175 171.5
176 159 172 181 175.5 165 163 173 170.5 171
(I)依据题目提示作出频率分布表;
(Ⅱ)在(I)的条件下画出频率分布直方图并且画出其频率分布折线图;
(Ⅲ)试利用频率分布的直方图估计样本的平均数。
【解】(I)最低身高156cm,最高身高184cm,确定组距为4,作频率分布表如下:
| 身高(cm) | 频数累计 | 频数 | 频率(%) |
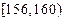 | | | |
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
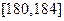 | | | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某中学研究性学习小组,为了考察高中学生的作文水平与爱看课外书的关系,在本校高三年级随机调查了 50名学生.调査结果表明:在爱看课外书的25人中有18人作文水平好,另7人作文水平一般;在不爱看课外书的25人中有6人作文水平好,另19人作文水平一般.
(Ⅰ)试根据以上数据完成以下2×2列联表,并运用独 立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
高中学生的作文水平与爱看课外书的2×2列联表
| | 爱看课外书 | 不爱看课外书 | 总计 |
作文水平 好 好 | | | |
| 作文水平一般 | [来源:学。科。网Z。X。X。K] | | |
| 总计 | | | |
 分别编号为1、2、3、4、5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
分别编号为1、2、3、4、5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.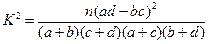 ,其中
,其中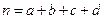 .
.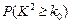 [来源:学*科*网] [来源:学*科*网] | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
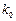 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com