
【题目】已知函数![]() ,有下列四个结论:
,有下列四个结论:
①![]() 为偶函数;②
为偶函数;②![]() 的值域为
的值域为![]() ;
;
③![]() 在
在![]() 上单调递减;④
上单调递减;④![]() 在
在![]() 上恰有8个零点,
上恰有8个零点,
其中所有正确结论的序号为( )
A.①③B.②④C.①②③D.①③④
【答案】A
【解析】
由偶函数的定义可判断①正确,借助二倍角公式将函数化简为 利用二次函数性质计算可得②错误,利用复合函数的单调性可判断
利用二次函数性质计算可得②错误,利用复合函数的单调性可判断![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,则
,则![]() 在
在![]() 上单调递增,根据偶函数性质可得出③正确,利用函数与方程的思想解方程即可判断④错误.
上单调递增,根据偶函数性质可得出③正确,利用函数与方程的思想解方程即可判断④错误.
由![]() ,故
,故![]() 为偶函数,①正确;
为偶函数,①正确; ,
,
记![]() ,则
,则 ,
,
当![]() 时,
时,![]() 取得最大值2,当
取得最大值2,当![]() 时,
时,![]() 取9得最小值
取9得最小值![]() ,
,
即 的值域为
的值域为![]() ,所以
,所以![]() 的值域为
的值域为![]() ,②错误;
,②错误;
![]() 在
在![]() 上的单调性与它在
上的单调性与它在![]() 上的单调性刚好相反,
上的单调性刚好相反,
当![]() 时,
时,![]() 单调递增,且
单调递增,且 ,而
,而 在
在 时单调递减,
时单调递减,
故![]() 在
在![]() 上单调递减,又此时
上单调递减,又此时 ,故函数
,故函数![]() 在
在![]() 上单调递增,于是得
上单调递增,于是得![]() 在
在![]() 单调递减,③正确;
单调递减,③正确;
令![]() ,得
,得![]() 或
或![]() ,而当
,而当![]() 时,
时,![]() 及
及![]() 恰有3个不等的实根
恰有3个不等的实根![]() ,
,![]() ,
,![]() ,
,
即![]() 在区间
在区间![]() 上恰有3个零点,结合奇偶性可知,即
上恰有3个零点,结合奇偶性可知,即![]() 在区间
在区间![]() 上恰有6个零点,④错误.
上恰有6个零点,④错误.
故正确的是①③.
故选:A.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
【题目】端午节是我国民间为纪念爱国诗人屈原的一个传统节日.某市为了解端午节期间粽子的销售情况,随机问卷调查了该市1000名消费者在去年端午节期间的粽子购买量(单位:克),所得数据如下表所示:
购买量 |
|
|
|
|
|
人数 | 100 | 300 | 400 | 150 | 50 |
将烦率视为概率
(1)试求消费者粽子购买量不低于300克的概率;
(2)若该市有100万名消费者,请估计该市今年在端午节期间应准备多少千克棕子才能满足市场需求(以各区间中点值作为该区间的购买量).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业质量检验员为了检测生产线上零件的质量情况,从生产线上随机抽取了![]() 个零件进行测量,根据所测量的零件尺寸(单位:mm),得到如下的频率分布直方图:
个零件进行测量,根据所测量的零件尺寸(单位:mm),得到如下的频率分布直方图:
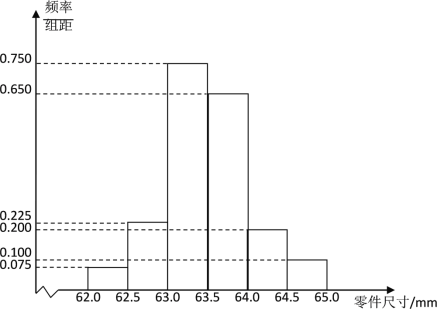
(1)根据频率分布直方图,求这![]() 个零件尺寸的中位数(结果精确到
个零件尺寸的中位数(结果精确到![]() );
);
(2)若从这![]() 个零件中尺寸位于
个零件中尺寸位于![]() 之外的零件中随机抽取
之外的零件中随机抽取![]() 个,设
个,设![]() 表示尺寸在
表示尺寸在![]() 上的零件个数,求
上的零件个数,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(3)已知尺寸在![]() 上的零件为一等品,否则为二等品,将这
上的零件为一等品,否则为二等品,将这![]() 个零件尺寸的样本频率视为概率. 现对生产线上生产的零件进行成箱包装出售,每箱
个零件尺寸的样本频率视为概率. 现对生产线上生产的零件进行成箱包装出售,每箱![]() 个. 企业在交付买家之前需要决策是否对每箱的所有零件进行检验,已知每个零件的检验费用为
个. 企业在交付买家之前需要决策是否对每箱的所有零件进行检验,已知每个零件的检验费用为![]() 元. 若检验,则将检验出的二等品更换为一等品;若不检验,如果有二等品进入买家手中,企业要向买家对每个二等品支付
元. 若检验,则将检验出的二等品更换为一等品;若不检验,如果有二等品进入买家手中,企业要向买家对每个二等品支付![]() 元的赔偿费用. 现对一箱零件随机抽检了
元的赔偿费用. 现对一箱零件随机抽检了![]() 个,结果有
个,结果有![]() 个二等品,以整箱检验费用与赔偿费用之和的期望值作为决策依据,该企业是否对该箱余下的所有零件进行检验?请说明理由.
个二等品,以整箱检验费用与赔偿费用之和的期望值作为决策依据,该企业是否对该箱余下的所有零件进行检验?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P与点![]() 的距离比它到直线
的距离比它到直线![]() 的距离小1.
的距离小1.
(1)求动点P的轨迹C的方程;
(2)设P为直线![]() 上任一点,过点P作曲线C的切线
上任一点,过点P作曲线C的切线![]() ,
,![]() ,切点分别为A,B,直线
,切点分别为A,B,直线![]() ,
,![]() 与y轴分别交于M,N两点,点
与y轴分别交于M,N两点,点![]() 、
、![]() 的纵坐标分别为m,n,求证:m与n的乘积为定值.
的纵坐标分别为m,n,求证:m与n的乘积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了比较两种治疗某病毒的药(分别称为甲药,乙药)的疗效,某医疗团队随机地选取了服用甲药的患者和服用乙药的患者进行研究,根据研究的数据,绘制了如图1等高条形图
.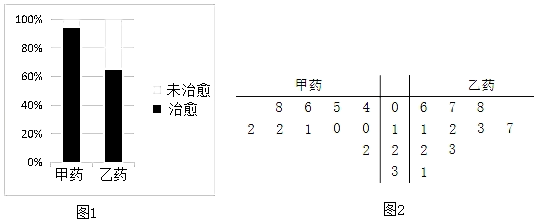
(1)根据等高条形图,判断哪一种药的治愈率更高,不用说明理由;
(2)为了进一步研究两种药的疗效,从服用甲药的治愈患者和服用乙药的治愈患者中,分别抽取了10名,记录他们的治疗时间(单位:天),统计并绘制了如图2茎叶图,从茎叶图看,哪一种药的疗效更好,并说明理由;
(3)标准差s除了可以用来刻画一组数据的离散程度外,还可以刻画每个数据偏离平均水平的程度,如果出现了治疗时间在(![]() 3s,
3s,![]() 3s)之外的患者,就认为病毒有可能发生了变异,需要对该患者进行进一步检查,若某服用甲药的患者已经治疗了26天还未痊愈,请结合(2)中甲药的数据,判断是否应该对该患者进行进一步检查?
3s)之外的患者,就认为病毒有可能发生了变异,需要对该患者进行进一步检查,若某服用甲药的患者已经治疗了26天还未痊愈,请结合(2)中甲药的数据,判断是否应该对该患者进行进一步检查?
参考公式:s![]() ,
,
参考数据:![]() 48.
48.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com