
【题目】若a、b是方程2lg2 x-lg x4+1=0的两个实根,求lg(ab)·![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】选修![]() :坐标系与参数方程
:坐标系与参数方程
已知曲线C的极坐标方程为ρ﹣4cosθ+3ρsin2θ=0,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l过点M(1,0),倾斜角为![]() .
.
(Ⅰ)求曲线C的直角坐标方程与直线l的参数方程;
(Ⅱ)若曲线C经过伸缩变换![]() 后得到曲线C′,且直线l与曲线C′交于A,B两点,求|MA|+|MB|.
后得到曲线C′,且直线l与曲线C′交于A,B两点,求|MA|+|MB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
有时可用函数
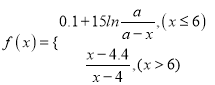
描述学习某学科知识的掌握程度,其中x表示某学科知识的学习次数(![]() ),
),![]() 表示对该学科知识的掌握程度,正实数a与学科知识有关.
表示对该学科知识的掌握程度,正实数a与学科知识有关.
(1) 证明:当![]() 时,掌握程度的增加量
时,掌握程度的增加量![]() 总是下降;
总是下降;
(2) 根据经验,学科甲、乙、丙对应的a的取值区间分别为![]() ,
,![]() ,
,
![]() .当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
.当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() (a>b>0)的离心率
(a>b>0)的离心率![]() ,过点
,过点![]() 和
和![]() 的直线与原点的距离为
的直线与原点的距离为![]() .
.

(1)求椭圆的方程.
(2)已知定点![]() ,若直线
,若直线![]() 与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国式过马路”是网友对部分中国人集体闯红灯现象的一种调侃,及“凑够一撮人就可以走了,和红绿灯无关”,某校研究性学习小组对全校学生按“跟从别人闯红灯”“从不闯红灯”“带头闯红灯”等三种形式进行调查获得下表数据:
跟从别人闯红灯 | 从不闯红灯 | 带头闯红灯 | |
男生 | 980 | 410 | 60 |
女生 | 340 | 150 | 60 |
用分层抽样的方法,从所有被调查的人中抽取一个容量为![]() 的样本,其中在“跟从别人闯红灯”的人中抽取了66人,
的样本,其中在“跟从别人闯红灯”的人中抽取了66人,
(Ⅰ) 求![]() 的值;
的值;
(Ⅱ)在所抽取的“带头闯红灯”的人中,任选取2人参加星期天社区组织的“文明交通”宣传活动,求这2人中至少有1人是女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若存在距离为
,若存在距离为![]() 的两条直线
的两条直线![]() 和
和![]() ,使得对任意
,使得对任意![]() 都有
都有![]() 恒成立,则称函数
恒成立,则称函数![]() 有一个宽度为
有一个宽度为![]() 的通道,给出下列函数:①
的通道,给出下列函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中在区间
.其中在区间![]() 上通道宽度可以为1的函数的个数是( )
上通道宽度可以为1的函数的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com