
【题目】已知函数![]() 图象的相邻两条对称轴之间的距离为
图象的相邻两条对称轴之间的距离为![]() .
.
(1)讨论函数f(x)在区间![]() 上的单调性;
上的单调性;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的![]() 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数![]() 的图象.求
的图象.求![]() 在
在![]() 上的值域.
上的值域.
【答案】(1)详见解析(2)![]()
【解析】
(1)首先利用二倍角公式、降次公式以及辅助角公式,将![]() 化简为
化简为![]() 的形式,利用相邻两条对称轴之间的距离得到半周期,从而求得
的形式,利用相邻两条对称轴之间的距离得到半周期,从而求得![]() 的值.再利用正弦函数的单调性求得函数在区间
的值.再利用正弦函数的单调性求得函数在区间![]() 上的递增和递减区间.(2)根据图像变换得到
上的递增和递减区间.(2)根据图像变换得到![]() 的表达式,然后利用定义域
的表达式,然后利用定义域![]() 的范围,利用三角函数值域的求法,来求得
的范围,利用三角函数值域的求法,来求得![]() 的值域.
的值域.
解:(1)f(x)=![]() -
-![]() +1=sin
+1=sin![]() +
+![]() ,因为相邻两条对称轴之间的距离为
,因为相邻两条对称轴之间的距离为![]() ,所以T=π,即
,所以T=π,即![]() =π,所以ω=1.
=π,所以ω=1.
故![]() .
.
若![]() ,则
,则![]() ,当
,当![]() ,即
,即![]() 时,
时,![]() 单调递增;
单调递增;
当![]() ,即
,即![]() 时,
时,![]() 单调递减.所以f(x)在区间
单调递减.所以f(x)在区间![]() 单调递增,在区间
单调递增,在区间![]() 单调递减.
单调递减.
(2)由(1)![]() ,将函数
,将函数![]() 的图象向左平移
的图象向左平移![]() 个单位得到,
个单位得到,![]()
![]() 的图象.再将所得图象各点的横坐标缩短为原来的
的图象.再将所得图象各点的横坐标缩短为原来的![]() 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数![]() 的图象.因此
的图象.因此![]() .
.
因为![]() ,所以
,所以![]() ,当
,当![]() 时,取得最大值
时,取得最大值![]() ;当
;当![]() 时,取得最小值
时,取得最小值![]() .
.
故![]() 在
在![]() 上的值域为
上的值域为![]() .
.


科目:高中数学 来源: 题型:
【题目】某中学对高二甲、乙两个同类班级进行“加强‘语文阅读理解’训练对提高‘数学应用题’得分率作用”的试验,其中甲班为试验班(加强语文阅读理解训练),乙班为对比班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用题测试的平均成绩(均取整数)如下表所示:
60分以下 | 60~70分 | 71~80分 | 81~90分 | 91~100分 | |
甲班/人数 | 3 | 6 | 11 | 18 | 12 |
乙班/人数 | 4 | 8 | 13 | 15 | 10 |
现规定平均成绩在80分以上(不含80分)的为优秀.参考公式及数据: .
.
| 0.05 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)试分别估计两个班级的优秀率;
(2)由以上统计数据填写下面![]() 列联表,并问是否有75%的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助.
列联表,并问是否有75%的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助.
优秀人数 | 非优秀人数 | 总计 | |
甲班 | |||
乙班 | |||
总计 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一商场对5年来春节期间服装类商品的优惠金额![]() (单位:万元)与销售额
(单位:万元)与销售额![]() (单位:万元)之间的关系进行分析研究并做了记录,得到如下表格.
(单位:万元)之间的关系进行分析研究并做了记录,得到如下表格.
日期 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)画出散点图,并判断服装类商品的优惠金额与销售额是正相关还是负相关;

(2)根据表中提供的数据,求出![]() 与
与![]() 的回归方程
的回归方程![]() ;
;
(3)若2019年春节期间商场预定的服装类商品的优惠金额为10万元,估计该商场服装类商品的销售额.
参考公式:
参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当今,手机已经成为人们不可或缺的交流工具,人们常常把喜欢玩手机的人冠上了名号“低头族”,手机已经严重影响了人们的生活.一媒体为调查市民对低头族的认识,从某社区的500名市民中随机抽取n名市民,按年龄情况进行统计的频率分布表和频率分布直方图如图:
组数 | 分组(单位:岁) | 频数 | 频率 |
1 |
| 5 | 0.05 |
2 |
| 20 | 0.20 |
3 |
| a | 0.35 |
4 |
| 30 | b |
5 |
| 10 | 0.10 |
合计 | n | 1.00 | |
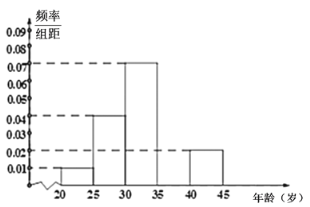
(1)求出表中a,b,n的值,并补全频率分布直方图;
(2)媒体记者为了做好调查工作,决定在第2,4,5组中用分层抽样的方法抽取6名市民进行问卷调查,再从这6名1民中随机抽取2名接受电视采访,求第2组至少有一名接受电视采访的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校医务室欲研究昼夜温差大小与高三患感冒人数多少之间的关系,他们统计了2019年9月至2020年1月每月8号的昼夜温差情况与高三因患感冒而就诊的人数,得到如下资料:
日期 | 2019年9月8日 | 2019年10月8日 | 2019年11月8日 | 2019年12月8日 | 2020年1月8日 |
昼夜温差 | 5 | 8 | 12 | 13 | 16 |
就诊人数 | 10 | 16 | 26 | 30 | 35 |
该医务室确定的研究方案是先从这5组数据中选取2组,用剩下的3组数据求线性回归方程,再用被选取的2组数据进行检验.假设选取的是2019年9月8日与2020年1月8日的2组数据.
(1)求就诊人数![]() 关于昼夜温差
关于昼夜温差![]() 的线性回归方程
的线性回归方程![]() (结果精确到0.01)
(结果精确到0.01)
(2)若由(1)中所求的线性回归方程得到的估计数据与所选出的检验数据的误差均不超过3人,则认为得到的线性回归方程是理想的,试问该医务室所得线性回归方程是否理想?
参考公式: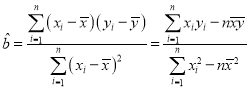 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某单位的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格全部卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了80个面包,以x(单位:个,![]() )表示面包的需求量,T(单位:元)表示利润.
)表示面包的需求量,T(单位:元)表示利润.

(1)求食堂面包需求量的平均数;
(2)求T关于x的函数解析式;
(3)根据直方图估计利润T不少于100元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() 的四个顶点围成的四边形面积为
的四个顶点围成的四边形面积为![]() .
.
(1)求![]() 的方程;
的方程;
(2)过![]() 的右焦点
的右焦点![]() ,且斜率不为0的直线
,且斜率不为0的直线![]() 与
与![]() 交于
交于![]() 两点,线段
两点,线段![]() 的垂直平分线经过点
的垂直平分线经过点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() .
.
(1)若椭圆![]() 的离心率为
的离心率为![]() ,求
,求![]() 的值;
的值;
(2)若过点![]() 任作一条直线
任作一条直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,在
,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() , 若存在,求出点
, 若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com