
已知函数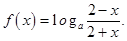 .
.
求(1) 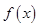 的定义域;
的定义域;
(2)判断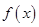 在其定义域上的奇偶性,并予以证明,
在其定义域上的奇偶性,并予以证明,
(3)求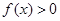 的解集。
的解集。
(1)定义域为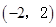 ;
;
(2)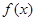 为定义域上的奇函数;
为定义域上的奇函数;
(3)a>1时,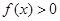 的解集为
的解集为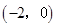 ,0<a<1时,
,0<a<1时,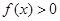 的解集为
的解集为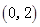 。
。
【解析】
试题分析:(1)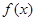 的定义域为
的定义域为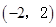
(2)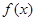 为定义域上的奇函数,
为定义域上的奇函数,
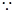
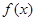 的定义域为
的定义域为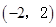 ,关于原点对称。
,关于原点对称。
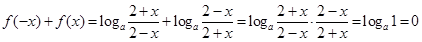
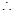
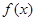 在
在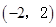 上为奇函数。
10
上为奇函数。
10
(3)a>1时,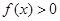 ,则
,则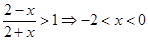 ,
,
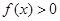 的解集为
的解集为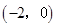
0<a<1时,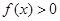 ,则
,则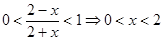 ,
,
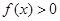 的解集为
的解集为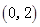 。
。
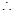 a>1时,
a>1时,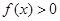 的解集为
的解集为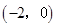
0<a<1时,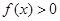 的解集为
的解集为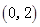 。
。
考点:本题主要考查函数的奇偶性、单调性,对数函数的性质,简单不等式的解法。
点评:中档题,研究函数的奇偶性,首先应看定义域是否关于原点对称,其次研究 的关系。涉及抽象不等式求解问题,一般要利用奇偶性、单调性,转化成具体不等式求解。涉及知识、对数函数问题,当底数不确定时,要讨论底数大于1、小于1的不同情况。
的关系。涉及抽象不等式求解问题,一般要利用奇偶性、单调性,转化成具体不等式求解。涉及知识、对数函数问题,当底数不确定时,要讨论底数大于1、小于1的不同情况。


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源:湖南省长沙一中、醴陵五中2008届高三第一次月考联合考试数学试卷 题型:044
已知函数![]() ,
,
求(1)函数f(x)最小正周期及最小值;
(2)函数在[0,π]上的单调递增区间.
查看答案和解析>>
科目:高中数学 来源:湖北省示范性高中孝昌二中2008届高三九月月考数学试卷(理科) 题型:044
已知函数![]() ,
,
求(1)函数f(x)最小正周期及最小值;
(2)函数在[0,∏]上的单调递增区间.
查看答案和解析>>
科目:高中数学 来源:黑龙江省鹤岗一中2009-2010学年高一上学期期末考试数学文科试题 题型:044
已知函数![]() ,求
,求
(1)函数y的最大值、最小值及最小正周期;
(2)函数y的单调递增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com