
【题目】(本小题满分13分)
如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(I)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(II)求证:![]() 平面
平面![]() ;
;
(II)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:本小题主要考查两条异面直线所成的角、直线与平面垂直、直线与平面所成的角等基础知识.考查空间想象能力、运算求解能力和推理论证能力.
试题解析:(Ⅰ)如图,由已知AD//BC,故![]() 或其补角即为异面直线AP与BC所成的角.因为AD⊥平面PDC,所以AD⊥PD.在Rt△PDA中,由已知,得
或其补角即为异面直线AP与BC所成的角.因为AD⊥平面PDC,所以AD⊥PD.在Rt△PDA中,由已知,得![]() ,故
,故![]() .
.
所以,异面直线AP与BC所成角的余弦值为![]() .
.
(Ⅱ)证明:因为AD⊥平面PDC,直线PD![]() 平面PDC,所以AD⊥PD.又因为BC//AD,所以PD⊥BC,又PD⊥PB,所以PD⊥平面PBC.
平面PDC,所以AD⊥PD.又因为BC//AD,所以PD⊥BC,又PD⊥PB,所以PD⊥平面PBC.
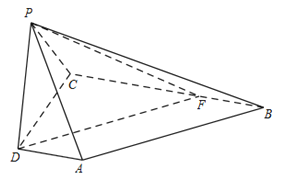
(Ⅲ)过点D作AB的平行线交BC于点F,连结PF,则DF与平面PBC所成的角等于AB与平面PBC所成的角.
因为PD⊥平面PBC,故PF为DF在平面PBC上的射影,所以![]() 为直线DF和平面PBC所成的角.
为直线DF和平面PBC所成的角.
由于AD//BC,DF//AB,故BF=AD=1,由已知,得CF=BC–BF=2.又AD⊥DC,故BC⊥DC,在Rt△DCF中,可得![]() .
.
所以,直线AB与平面PBC所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】(本题满分15分)如图,已知抛物线![]() ,点A
,点A![]() ,
,![]() ,抛物线上的点
,抛物线上的点![]() .过点B作直线AP的垂线,垂足为Q.
.过点B作直线AP的垂线,垂足为Q.

(Ⅰ)求直线AP斜率的取值范围;
(Ⅱ)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() sinxcosx﹣2cos2x+1.
sinxcosx﹣2cos2x+1.
(1)求函数f(x)的最小正周期;
(2)将函数f(x)的图象向左平移 ![]() 个单位,得到函数g(x)的图象.在△ABC中,角A,B,C的对边分别为a,b,c,若g(
个单位,得到函数g(x)的图象.在△ABC中,角A,B,C的对边分别为a,b,c,若g( ![]() )=1,a=2,b+c=4,求△ABC的面积.
)=1,a=2,b+c=4,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二项式![]() 的展开式中只有第6项的二项式系数最大,且展开式中的第3项的系数是第4项的系数的3倍,则
的展开式中只有第6项的二项式系数最大,且展开式中的第3项的系数是第4项的系数的3倍,则![]() 的值为( )
的值为( )
A. 4 B. 8 C. 12 D. 16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC各顶点的坐标分别为:A(0,4);B(﹣3,0),C(1,1)
(1)求点C到直线AB的距离;
(2)求AB边的高所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(18)(本小题满分12分)在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙中心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者A1,A2,A3,A4,A5,A6和4名B1,B2,
B3,B4,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示。
(I)求接受甲种心理暗示的志愿者中包含A1但不包含B3的频率。
(II)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望EX。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系中![]() 轴的正半轴重合.若曲线
轴的正半轴重合.若曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 的参数方程化为极坐标方程;
的参数方程化为极坐标方程;
(2)由直线![]() 上一点向曲线
上一点向曲线![]() 引切线,求切线长的最小值.
引切线,求切线长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在多面体![]() 中,
中, ![]() 与
与![]() 均为边长为2的正方形,
均为边长为2的正方形, ![]() 为等腰直角三角形,
为等腰直角三角形, ![]() ,且平面
,且平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com