Question

【题目】【2018山西晋城市高三上学期一模】环境问题是当今世界共同关注的问题，我国环保总局根据空气污染指数浓度，制定了空气质量标准：

空气污染指数
空气质量等级	优	良	轻度污染	中度污染	重度污染	严重污染

某市政府为了打造美丽城市，节能减排，从2010年开始考察了连续六年11月份的空气污染指数，绘制了频率分布直方图，经过分析研究，决定从2016年11月1日起在空气质量重度污染和严重污染的日子对机动车辆限号出行，即车牌尾号为单号的车辆单号出行，车牌尾号为双号的车辆双号出行（尾号是字母的，前13个视为单号，后13个视为双号），王先生有一辆车，若11月份被限行的概率为0．05．

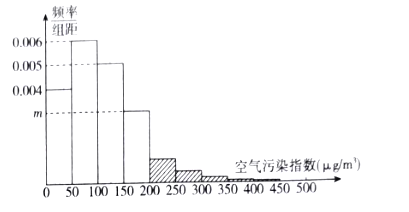
（I）求频率分布直方图中的值（写出推理过程，直接写出答案不得分）；

（II）若按分层抽样的方法，从空气质量良好与中度污染的天气中抽取6天，再从这6天中随机抽取2天，求至少有一天空气质量中度污染的概率；

（III）该市环保局为了调查汽车尾气排放对空气质量的影响，对限行两年来的11月份共60天的空气质量进行统计，其结果如下表：

根据限行前6年180天与限行后60天的数据，计算并填写以下列联表，并回答是否有的把握认为空气质量的优良与汽车尾气的排放有关．

参考数据：

参考公式：，其中．

Answer 1

【答案】（I）0．003；（II）；（III）至少有的把握认为空气质量的优良与汽车尾气的排放有关．

【解析】试题分析：

（1）由题意可得空气重度污染和严重污染的概率应为，然后根据频率分布直方图中所有小长方形的面积和为1可求得．（2）由题意得空气质量良好与中度污染的天气的概率之比为，故根据分层抽样抽取6天，则空气质量良好天气被抽取4天，空气中度污染天气被抽取2天，然后列举出所有的可能结果，根据古典概型概率公式求解．（3）由条件得到列联表，由此求得，然后结合所给的参考数据得到结论．

试题解析：

（1）因为限行分单双号，王先生的车被限行的概率为0.05，

所以空气重度污染和严重污染的概率应为，

由频率分布直方图可知：

，

解得.

（2）因为空气质量良好与中度污染的天气的概率之比为，

按分层抽样从中抽取6天，则空气质量良好天气被抽取4天，记做，

空气中度污染天气被抽取2天，记做，

从这6天中随机抽取2天，所包含的基本事件有： ，共15个．

记事件为“至少有一天空气质量中度污染”，则事件所包含的基本事件有： ，共9个，

故.

即至少有一天空气质量中度污染的概率为．

（3）列联表如下：

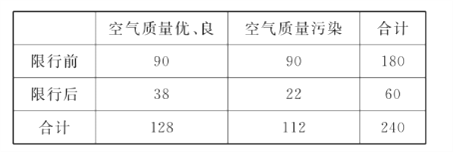
由表中数据可得 ，

所以至少有的把握认为空气质量的优良与汽车尾气的排放有关.