(1)求过直线x+y+4=0与x-y+2=0的交点,且平行于直线 x-2y=0的直线方程.
(2)设直线4x+3y+1=0和圆x2+y2-2x-3=0相交于点A、B,求弦AB的长及其垂直平分线的方程.
(3)过点P(3,0)有一条直线l,它夹在两条直线l1:2x-y-2=0与l2:x+y+3=0之间的线段恰被P点平分,求直线l的方程.
【答案】
分析:(1)先联立直线x+y+4=0与x-y+2=0的方程,求交点坐标,因为所求直线平行于直线 x-2y=0,所以斜率与直线x-2y=0的斜率相等,求出斜率,再用点斜式写出方程,化为一般式即可.
(2)把圆方程化为标准方程,求出圆心坐标和半径,再求出圆心到直线4x+3y+1=0的距离,在圆中,半径,半弦,弦心距构成直角三角形,满足勾股定理,就可求出半弦的值,进而求出弦AB的长.
直线l的垂直平分线斜率等于直线l的斜率的负倒数,且过圆心,用点斜式求出方程即可.
(3)先设出M与N两点的坐标,因为P为线段MN的中点,利用中点坐标公式即可列出两点坐标的两个关系式,然后把M的坐标代入直线l
1,把B的坐标代入直线l
2,又得到两点坐标的两个关系式,把四个关系式联立即可求出M的坐标,然后由M和P的坐标,利用两点式即可写出直线l的方程.
解答:解:(1)解方程组
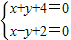
,得
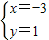
∴交点坐标为(-3,1),
又∵所求直线平行于直线 x-2y=0,∴斜率为

∴直线方程为y-1=

(x+3),即x-2y+5=0
(2)圆x
2+y
2-2x-3=0可化为(x-1)
2+y
2=4,∴圆心C的坐标为(1,0),半径为2.
圆心C到直线4x+3y+1=0的距离d=
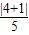
=1
∴

|AB|=
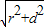
=
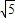
,
∴|AB|=2
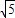
∵直线l的斜率为-

,∴垂直平分线的斜率为

又∵直线l的垂直平分线过圆心(1,0),∴方程为y=

(x-1)
化简得,3x-4y-3=0
(3)设直线l夹在直线l
1,l
2之间的部分是MN,且MN被P(3,0)平分.
设点M,N的坐标分别是(x
1,y
1),(x
2,y
2),则有
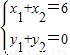
又∵M,N两点分别在直线l
1,l
2上,∴
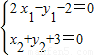
由上述四个式子得 x
1=
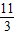
,y
1=
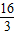
,即M点坐标是(
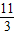
,
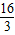
),
∴直线l的方程为8x-y-24=0.
点评:此题考查了两直线交点的求法,直线平行的充要条件的应用,圆中弦长的求法,直线之间关系的判断,做题时要灵活运用所学知识进行计算.

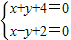 ,得
,得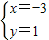

 (x+3),即x-2y+5=0
(x+3),即x-2y+5=0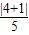 =1
=1 |AB|=
|AB|=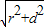 =
=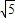 ,
,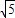
 ,∴垂直平分线的斜率为
,∴垂直平分线的斜率为
 (x-1)
(x-1)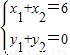
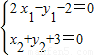
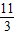 ,y1=
,y1=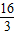 ,即M点坐标是(
,即M点坐标是(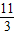 ,
,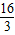 ),
),
